Core Algorithms
Use Nonparametric Distributions to Simulate Natural Processes
A data-based distribution created using Old Faithful geyser data. Here one visualizes the PDF and a random sample drawn from the distribution.
| In[1]:= | X |
| In[2]:= | X |
| In[3]:= |  X |
| Out[3]= | 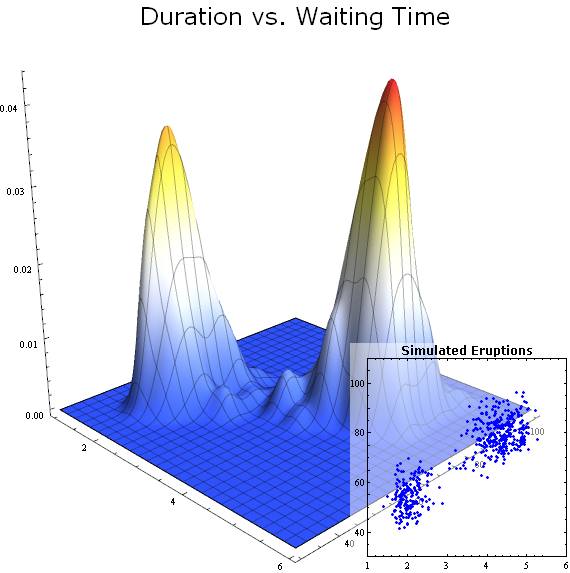 |