Core Algorithms
Test for Goodness-of-Fit to Any Distribution or Dataset
Visually compare adaptive kernel density estimates to parametric distributions and assess the fit with any one of over a dozen goodness-of-fit tests.
| In[1]:= |  X |
| In[2]:= |  X |
| In[3]:= |  X |
| In[4]:= | X |
| Out[4]= | 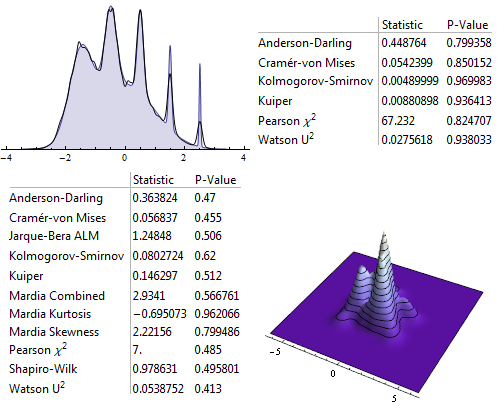 |