Core Algorithms
Visualize Optimal Parameter Values
Fit data to a Weibull distribution using maximum likelihood and visualize the optimal point in contour and 3D plots of the log-likelihood.
| In[1]:= | X |
| In[2]:= | X |
| In[3]:= |  X |
| Out[3]= | 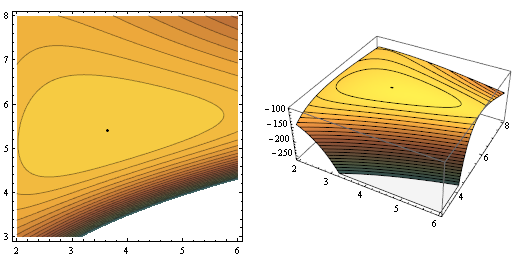 |
| New in Wolfram Mathematica 8: Parameter Estimation and Testing | ◄ previous | next ► |
| In[1]:= | X |
| In[2]:= | X |
| In[3]:= |  X |
| Out[3]= |  |