Core Algorithms
English Is Not a Random Set of Words
The length of words in English follows a BinomialDistribution—the fit is shown on the first picture. The collection of words with random length can be modeled well by a WaringYuleDistribution, as the second graphic shows.
| In[1]:= | X |
| In[2]:= |  X |
| In[3]:= | 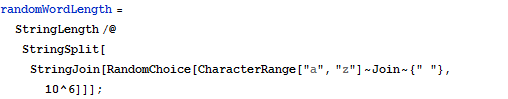 X |
| In[4]:= | X |
| In[5]:= |  X |
| Out[5]= | 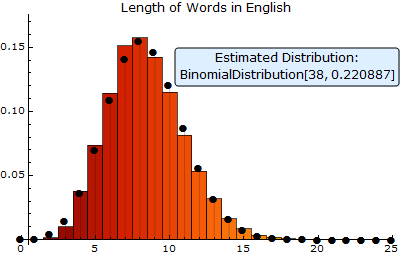 |
| Out[5]= | 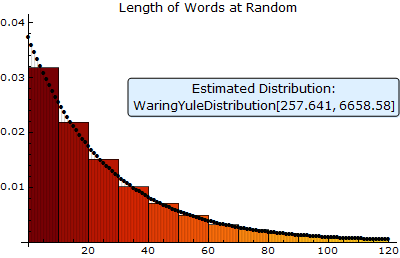 |