Core Algorithms
Compare Two Distributions with the Same Moment Sequence
Use varying scales to see fine-grained detail and general shapes of PDFs for two different distributions with equivalent moments, and compare their first several moments in tables.
| In[1]:= | 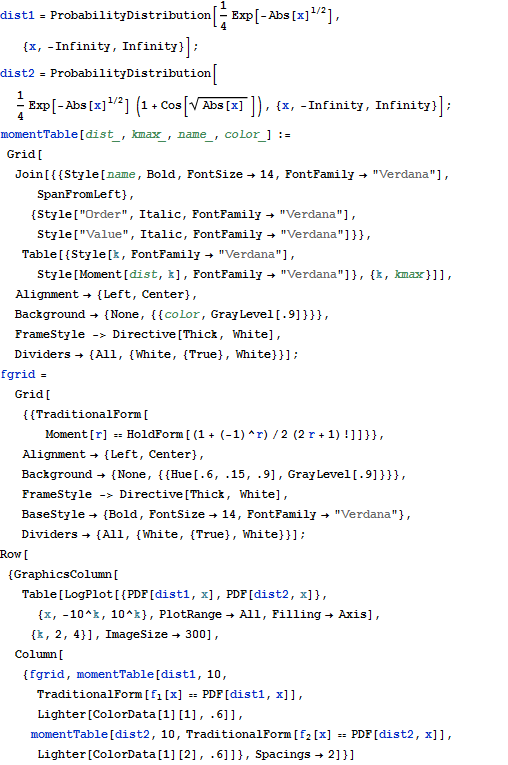 X |
| Out[1]= | 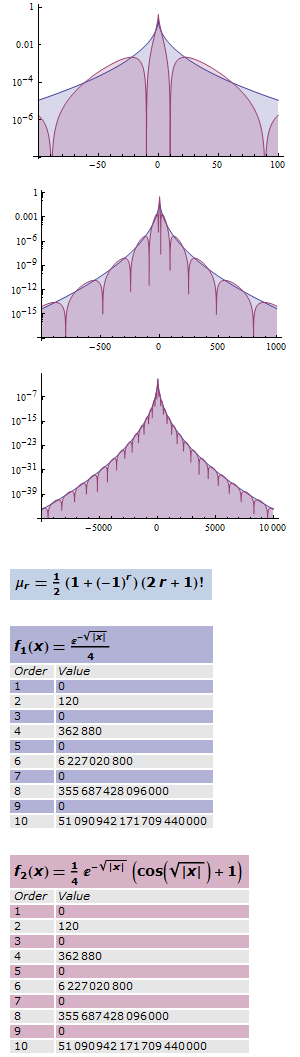 |