Core Algorithms
Compute the Probability of an Event
Compute the probabilities of events in parametric, nonparametric, derived, or formula distributions.
| In[1]:= |  X |
| In[2]:= |  X |
| In[3]:= | X |
| Out[3]= | 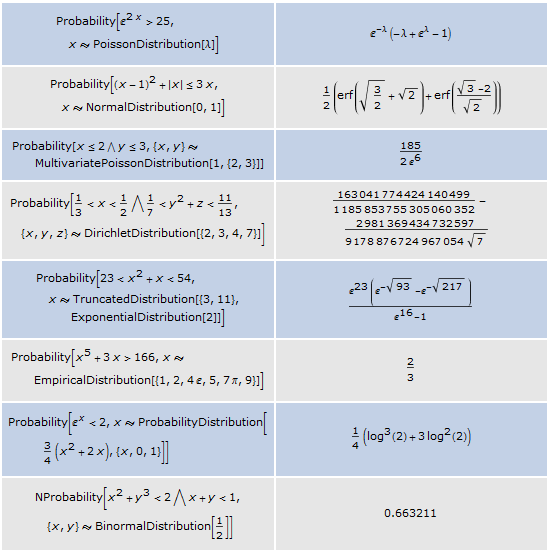 |
| New in Wolfram Mathematica 8: Probability and Statistics Solvers and Properties | ◄ previous | next ► |
| In[1]:= |  X |
| In[2]:= |  X |
| In[3]:= | X |
| Out[3]= |  |