Time-Delay Systems 

Time-delay systems can be specified in multiple ways and conveniently converted between state-space and transfer-function representations.

A time-delay system specified as an ODE.

In[1]:=

X StateSpaceModel[x'[t] + x[t - 1] == 2 u[t] + u[t - 3], x[t], u[t], x[t], t]

Out[1]=

A system specified using state-space matrices and the SystemsModelDelay operator.

In[2]:=

X StateSpaceModel[{{{-SystemsModelDelay[2]}}, {{3 + SystemsModelDelay[1]}}, {{1}}, {{0}}}]

Out[2]=

A system specified as a transfer function.

In[3]:=

X TransferFunctionModel[(3 + Exp[-s])/(s + Exp[-2 s]), s]

Out[3]=

A transfer function with delays specified using SystemsModelDelay.

In[4]:=

X TransferFunctionModel[(3 + SystemsModelDelay[1])/( s + SystemsModelDelay[2]), s]

Out[4]=

A discrete-time system is determined with the SamplingPeriod option.

In[5]:=

X StateSpaceModel[{{{-SystemsModelDelay[2]}}, {{3 + SystemsModelDelay[1]}}, {{1}}, {{0}}}, SamplingPeriod -> 2]

Out[5]=

In[6]:=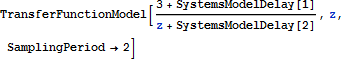

X TransferFunctionModel[(3 + SystemsModelDelay[1])/( z + SystemsModelDelay[2]), z, SamplingPeriod -> 2]

Out[6]=

Convert between state-space and transfer-function representations.

In[7]:=

X StateSpaceModel[ TransferFunctionModel[{{{3 + SystemsModelDelay[1]}}, s + SystemsModelDelay[2]}, s]]

Out[7]=

In[8]:=

X TransferFunctionModel[ StateSpaceModel[{{{-SystemsModelDelay[2]}}, {{3 + SystemsModelDelay[ 1]}}, {{1}}, {{0}}}, SamplingPeriod -> 2, SystemsModelLabels -> None], z]

Out[8]=

Obtain the discrete-time approximations of continuous-time systems and vice versa.

In[9]:=

X ToContinuousTimeModel[ StateSpaceModel[{{{-SystemsModelDelay[2]}}, {{1}}, {{3 + SystemsModelDelay[1]}}, {{0}}}, SamplingPeriod -> 2, SystemsModelLabels -> None], Method -> "BilinearTransform"]

Out[9]=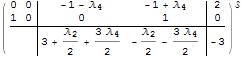

In[10]:=

X ToDiscreteTimeModel[ StateSpaceModel[{{{-SystemsModelDelay[1]}}, {{2 + SystemsModelDelay[ 3]}}, {{1}}, {{0}}}, SamplingPeriod ->None, SystemsModelLabels -> None], 2]

Out[10]=