Evaluate Infinite Sums in Terms of Mittag-Leffler's E Function 

Evaluate infinite sums with symbolic parameters in terms of MittagLefflerE.

In[1]:=

X Sum[z^k/Gamma[\[Alpha] k + 1], {k, 0, \[Infinity]}]

Out[1]=

In[2]:=

X Sum[z^k/Gamma[\[Alpha] k + \[Beta]], {k, 0, \[Infinity]}]

Out[2]=

The answer simplifies for special values of the parameters.

In[3]:=

X Sum[z^k/Gamma[\[Alpha] k + \[Beta]], {k, 0, \[Infinity]}]; % /. {z -> 1, \[Alpha] -> 2, \[Beta] -> 1}

Out[3]=

In[4]:=

X Sum[1/Gamma[2 k + 1], {k, 0, \[Infinity]}]

Out[4]=

Out[10]//TraditionalForm=
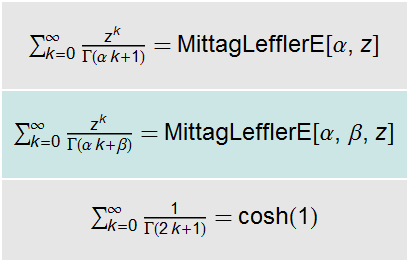