Distribution of Times to Reach a Target State 

Compute the PDF, CDF, mean, and variance for the number of steps needed to go from state 1 to state 3.

In[1]:=

X \[ScriptCapitalP] = DiscreteMarkovProcess[1, ({ {0, 1/2, 1/2}, {1/2, 0, 1/2}, {1/2, 1/2, 0} })];

In[2]:=

X \[ScriptCapitalD] = FirstPassageTimeDistribution[\[ScriptCapitalP], 3];

Probability density function.

In[3]:=

X PDF[\[ScriptCapitalD], k]

Out[3]=

In[4]:=

X PDF[\[ScriptCapitalD], k]; DiscretePlot[%, {k, 1, 5}, ExtentSize -> 1/2]

Out[4]=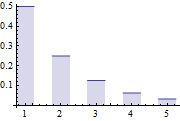

Cumulative distribution function.

In[5]:=

X CDF[\[ScriptCapitalD], k]

Out[5]=

In[6]:=

X CDF[\[ScriptCapitalD], k]; DiscretePlot[%, {k, 0, 5}, ExtentSize -> Right]

Out[6]=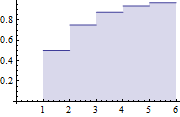

Mean and variance.

In[7]:=

X Mean[\[ScriptCapitalD]]

Out[7]=

In[8]:=

X Variance[\[ScriptCapitalD]]

Out[8]=