Voting Power in a Presidential Election
| In[1]:= |  X |
| In[2]:= | 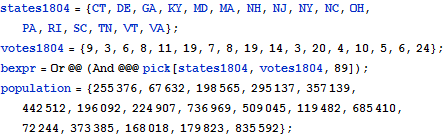 X |
| In[3]:= | X |
| In[4]:= | 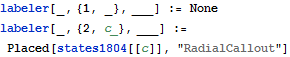 X |
| In[5]:= |  X |
Compare the Banzhaf power index, which is another name for StructuralImportance, of the states in the 1804 US presidential election with their population.
| Out[5]= | 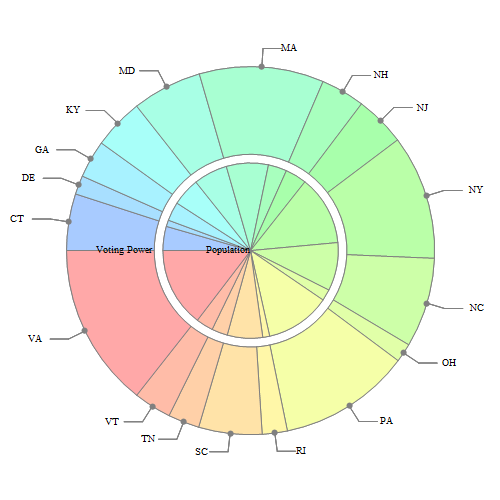 |