Cliques and Cohesive Groups
Compute components, cliques, and cohesive groups in a network.
| In[1]:= | 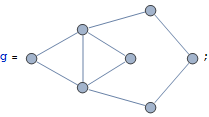 X |
| In[1]:= | X |
| In[1]:= | 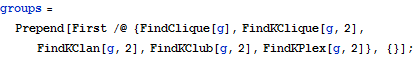 X |
| In[1]:= |  X |
| In[2]:= | X |
| In[3]:= |  X |
| In[4]:= | X |
| In[5]:= | X |
| In[6]:= | 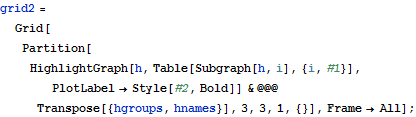 X |
| In[7]:= | X |
| Out[7]= | 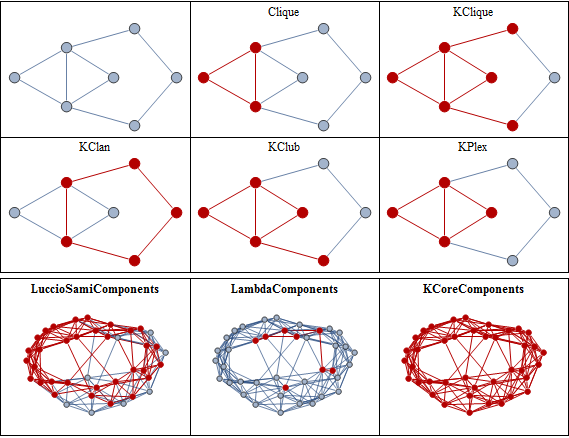 |
| « View all new features in Mathematica 9 | ◄ previous | next ► |
| In[1]:= |  X |
| In[1]:= | X |
| In[1]:= | 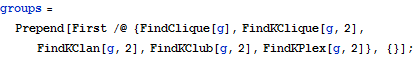 X |
| In[1]:= |  X |
| In[2]:= | X |
| In[3]:= |  X |
| In[4]:= | X |
| In[5]:= | X |
| In[6]:= |  X |
| In[7]:= | X |
| Out[7]= |  |