Find Conditions for Stationarity and Invertibility of Time Series Processes 

Find conditions for an ARMAProcess[2, 2] to be weakly stationary using WeakStationarity.

In[1]:=

X arma = ARMAProcess[{Subscript[a, 1], Subscript[a, 2]}, {Subscript[b, 1], Subscript[b, 2]}, \[Sigma]]; ws = WeakStationarity[arma]

Out[1]=

In[2]:=

X RegionPlot[ws, {Subscript[a, 1], -2, 2}, {Subscript[a, 2], -2, 2}, GridLines -> Automatic]

Out[2]=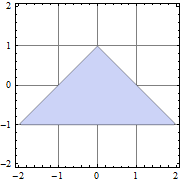

Find an instance of a weakly stationary ARMAProcess[2, 2].

In[3]:=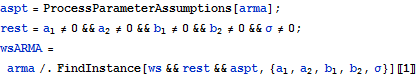

X aspt = ProcessParameterAssumptions[arma]; rest = Subscript[a, 1] != 0 && Subscript[a, 2] != 0 && Subscript[b, 1] != 0 && Subscript[b, 2] != 0 && \[Sigma] != 0; wsARMA = arma /. FindInstance[ ws && rest && aspt, {Subscript[a, 1], Subscript[a, 2], Subscript[ b, 1], Subscript[b, 2], \[Sigma]}][[1]]

Out[3]=

Check that the process is weakly stationary.

In[4]:=

X WeakStationarity[wsARMA]

Out[4]=

Find conditions for an ARMAProcess[2, 2] to be invertible using TimeSeriesInvertibility.

In[5]:=

X in = TimeSeriesInvertibility[arma]

Out[5]=

In[6]:=

X RegionPlot[in, {Subscript[b, 1], -2, 2}, {Subscript[b, 2], -2, 2}, GridLines -> Automatic]

Out[6]=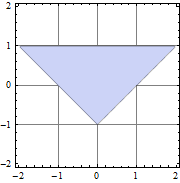

Find an instance of an invertible ARMAProcess[2, 2].

In[7]:=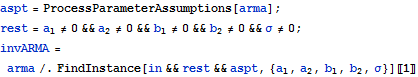

X aspt = ProcessParameterAssumptions[arma]; rest = Subscript[a, 1] != 0 && Subscript[a, 2] != 0 && Subscript[b, 1] != 0 && Subscript[b, 2] != 0 && \[Sigma] != 0; invARMA = arma /. FindInstance[ in && rest && aspt, {Subscript[a, 1], Subscript[a, 2], Subscript[ b, 1], Subscript[b, 2], \[Sigma]}][[1]]

Out[7]=

Check that the process is invertible.

In[8]:=

X TimeSeriesInvertibility[invARMA]

Out[8]=