Perform Dimensional Analysis

Use the Buckingham

theorem to find non-dimensional expressions.

In[1]:=

setupBPT[terms_List] := 
 With[{ud = Union[Flatten[UnitDimensions /@ terms, 1][[All, 1]]]}, 
  If[MemberQ[ud, _UnitDimensions], 
   Throw[None]]; {Length@terms - Length[ud], ud}]
UDToExp[dimensions_List] := 
 Times @@ (dimensions /. List[d_String, n_] :> Power[d, n])
Nondimensionalize[expr_, vars_List] := 
 With[{exp = 
    expr /. {Power[q_Quantity, n_] :> UDToExp[UnitDimensions[q]]^n, 
      qu_Quantity :> UDToExp[UnitDimensions[qu]]}}, 
  With[{res = 
     Solve[Thread[((List @@ PowerExpand[exp]) /. 
          Power[unit_String, n_] :> n) == 0], vars]}, 
   If[Flatten[res] === {}, Throw[None], 
    With[{nondim = expr /. q_Quantity :> QuantityMagnitude[q]}, 
     First[nondim /. res]]]]]
Buckingham\[Pi][terms_List, const : {__Integer}] := 
 Catch[With[{res = setupBPT[terms]}, 
     If[Length[Union[const]] =!= First[res], Throw[None]]; 
     If[MemberQ[const, x_ /; x > Length[terms]], Throw[None]]; 
     With[{c = #}, 
      Module[{temp, vars = {}}, 
       Check[temp = 
         If[Not[MemberQ[const, #]], 
            With[{u = Unique[]}, AppendTo[vars, u]; terms[[#]]^u], 
            If[c =!= #, 1, terms[[#]]]] & /@ Range[Length[terms]], 
        Throw[None], {Part::partw}]; 
       Nondimensionalize[Times @@ temp, vars]]]] & /@ const]

Find the various non-dimensional expressions associated with the following five physical quantities.

In[2]:=

In[3]:=

Out[3]//MatrixForm=
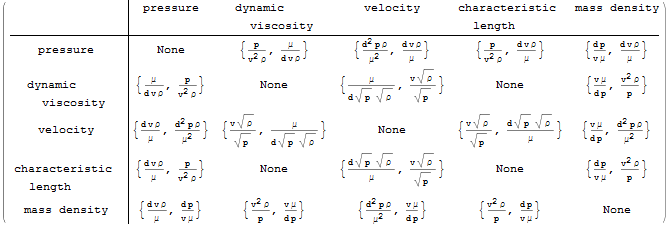