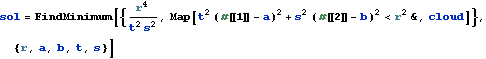| New in Wolfram Mathematica 6: Constrained Nonlinear Optimization | ◄ previous | next ► |
Handle Systems of Nonlinear Constraints
Mathematica 6 can minimize nonlinear functions with many variables and large numbers of nonlinear constraints. Here it finds the ellipse of minimum area that encloses a given collection of points.
In[1]:= | cloud = (# {1, .5}) & /@ RandomReal[NormalDistribution[], {200, 2}]; |
In[2]:= | sol = FindMinimum[{r^4/(t^2 s^2),
Map[t^2 (#[[1]] - a)^2 + s^2 (#[[2]] - b)^2 < r^2 &, cloud]}, {r,
a, b, t, s}] |
Out[2]=  |
In[3]:= | RegionPlot[(t^2 (x - a)^2 + s^2 (y - b)^2 < r^2) /. Last[sol], {x, -3,
3}, {y, -3, 3}, Epilog -> Point[cloud]] |
Out[3]=  | 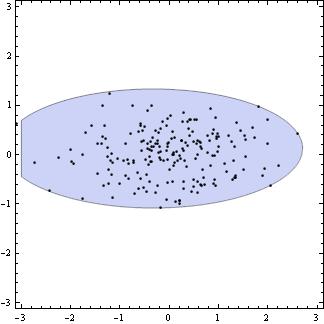 |