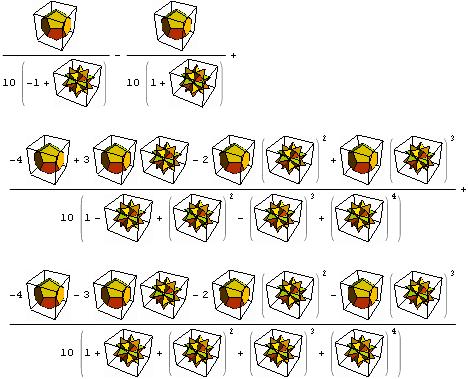
Apart[\!\(\*
Graphics3DBox[
{RGBColor[1, 1, 0],
GraphicsComplex3DBox[
NCache[{{
0, 0, (Rational[
9, 8] + Rational[3, 8] 5^Rational[1, 2])^Rational[1, 2]}, {
0, 0, Rational[-1, 2] (
Rational[3, 2] (3 + 5^Rational[1, 2]))^Rational[1, 2]}, {(
Rational[
1, 8] + Rational[-1, 24] 5^Rational[1, 2])^Rational[1, 2],
Rational[1, 4] (-3 - 5^Rational[1, 2]), (
Rational[1, 8] + Rational[1, 24] 5^Rational[1, 2])^Rational[
1, 2]}, {(
Rational[
1, 8] + Rational[-1, 24] 5^Rational[1, 2])^Rational[1, 2],
Rational[1, 4] (3 + 5^Rational[1, 2]), (
Rational[1, 8] + Rational[1, 24] 5^Rational[1, 2])^Rational[
1, 2]}, {(
Rational[1, 8] + Rational[1, 24] 5^Rational[1, 2])^Rational[
1, 2], Rational[1, 4] (-1 - 5^Rational[1, 2]),
Rational[-1, 2] (
Rational[5, 6] (3 + 5^Rational[1, 2]))^Rational[1, 2]}, {(
Rational[1, 8] + Rational[1, 24] 5^Rational[1, 2])^Rational[
1, 2], Rational[1, 4] (1 + 5^Rational[1, 2]),
Rational[-1, 2] (
Rational[5, 6] (3 + 5^Rational[1, 2]))^Rational[1, 2]}, {(
Rational[5, 8] + Rational[5, 24] 5^Rational[1, 2])^Rational[
1, 2], Rational[1, 4] (-1 - 5^Rational[1, 2]), (
Rational[1, 8] + Rational[1, 24] 5^Rational[1, 2])^Rational[
1, 2]}, {(
Rational[5, 8] + Rational[5, 24] 5^Rational[1, 2])^Rational[
1, 2], Rational[1, 4] (1 + 5^Rational[1, 2]), (
Rational[1, 8] + Rational[1, 24] 5^Rational[1, 2])^Rational[
1, 2]}, {-(
Rational[3, 4] + Rational[1, 3] 5^Rational[1, 2])^Rational[
1, 2], Rational[-1, 2], (
Rational[1, 8] + Rational[1, 24] 5^Rational[1, 2])^Rational[
1, 2]}, {-(
Rational[3, 4] + Rational[1, 3] 5^Rational[1, 2])^Rational[
1, 2], Rational[
1, 2], (Rational[
1, 8] + Rational[1, 24] 5^Rational[1, 2])^Rational[
1, 2]}, {(
Rational[3, 4] + Rational[1, 3] 5^Rational[1, 2])^Rational[
1, 2], Rational[-1, 2],
Rational[-1, 2] (
Rational[1, 6] (3 + 5^Rational[1, 2]))^Rational[1, 2]}, {(
Rational[3, 4] + Rational[1, 3] 5^Rational[1, 2])^Rational[
1, 2], Rational[1, 2],
Rational[-1, 2] (
Rational[1, 6] (3 + 5^Rational[1, 2]))^Rational[1, 2]}, {-(
Rational[1, 6] (3 + 5^Rational[1, 2]))^Rational[1, 2], 0,
Rational[-1, 2] (
Rational[5, 6] (3 + 5^Rational[1, 2]))^Rational[1, 2]}, {
Rational[-1, 2] (
Rational[1, 6] (3 + 5^Rational[1, 2]))^Rational[1, 2],
Rational[1, 4] (-1 - 5^Rational[1, 2]), (
Rational[5, 8] + Rational[5, 24] 5^Rational[1, 2])^Rational[
1, 2]}, {
Rational[-1, 2] (
Rational[1, 6] (3 + 5^Rational[1, 2]))^Rational[1, 2],
Rational[1, 4] (1 + 5^Rational[1, 2]), (
Rational[5, 8] + Rational[5, 24] 5^Rational[1, 2])^Rational[
1, 2]}, {(Rational[1, 6] (3 + 5^Rational[1, 2]))^Rational[
1, 2], 0, (
Rational[5, 8] + Rational[5, 24] 5^Rational[1, 2])^Rational[
1, 2]}, {
Rational[-1, 2] (
Rational[5, 6] (3 + 5^Rational[1, 2]))^Rational[1, 2],
Rational[1, 4] (-1 - 5^Rational[1, 2]),
Rational[-1, 2] (
Rational[1, 6] (3 + 5^Rational[1, 2]))^Rational[1, 2]}, {
Rational[-1, 2] (
Rational[5, 6] (3 + 5^Rational[1, 2]))^Rational[1, 2],
Rational[1, 4] (1 + 5^Rational[1, 2]),
Rational[-1, 2] (
Rational[1, 6] (3 + 5^Rational[1, 2]))^Rational[1, 2]}, {
Root[1 - 36 #^2 + 144 #^4& , 2, 0],
Rational[1, 4] (-3 - 5^Rational[1, 2]),
Rational[-1, 2] (
Rational[1, 6] (3 + 5^Rational[1, 2]))^Rational[1, 2]}, {
Root[1 - 36 #^2 + 144 #^4& , 2, 0],
Rational[1, 4] (3 + 5^Rational[1, 2]),
Rational[-1, 2] (
Rational[1, 6] (3 + 5^Rational[1, 2]))^Rational[1, 2]}}, {{
0, 0, 1.4012585384440737`}, {0, 0, -1.4012585384440737`}, {
0.17841104488654497`, -1.3090169943749475`,
0.46708617948135783`}, {0.17841104488654497`,
1.3090169943749475`, 0.46708617948135783`}, {
0.46708617948135783`, -0.8090169943749475, \
-1.0444364486709836`}, {0.46708617948135783`,
0.8090169943749475, -1.0444364486709836`}, {
1.0444364486709836`, -0.8090169943749475,
0.46708617948135783`}, {1.0444364486709836`,
0.8090169943749475,
0.46708617948135783`}, {-1.2228474935575286`, -0.5,
0.46708617948135783`}, {-1.2228474935575286`, 0.5,
0.46708617948135783`}, {
1.2228474935575286`, -0.5, -0.46708617948135783`}, {
1.2228474935575286`,
0.5, -0.46708617948135783`}, {-0.9341723589627157,
0, -1.0444364486709836`}, {-0.46708617948135783`, \
-0.8090169943749475, 1.0444364486709836`}, {-0.46708617948135783`,
0.8090169943749475, 1.0444364486709836`}, {
0.9341723589627157, 0,
1.0444364486709836`}, {-1.0444364486709836`, \
-0.8090169943749475, -0.46708617948135783`}, {-1.0444364486709836`,
0.8090169943749475, -0.46708617948135783`}, \
{-0.17841104488654494`, -1.3090169943749475`, -0.46708617948135783`}, \
{-0.17841104488654494`, 1.3090169943749475`, -0.46708617948135783`}}],
Polygon3DBox[{{15, 10, 9, 14, 1}, {2, 6, 12, 11, 5}, {5, 11, 7,
3, 19}, {11, 12, 8, 16, 7}, {12, 6, 20, 4, 8}, {6, 2, 13, 18,
20}, {2, 5, 19, 17, 13}, {4, 20, 18, 10, 15}, {18, 13, 17, 9,
10}, {17, 19, 3, 14, 9}, {3, 7, 16, 1, 14}, {16, 8, 4, 15,
1}}]]},
ImageSize->{44., Automatic}]\)/(\!\(\*
Graphics3DBox[
{RGBColor[1, 1, 0],
GraphicsComplex3DBox[
NCache[{{0, 0, Root[5 - 20 #^2 + 16 #^4& , 1, 0]}, {
0, 0, Root[5 - 20 #^2 + 16 #^4& , 4, 0]}, {
Root[1 - 5 #^2 + 5 #^4& , 1, 0], 0, Root[
1 - 20 #^2 + 80 #^4& , 1, 0]}, {
Root[1 - 5 #^2 + 5 #^4& , 4, 0], 0, Root[
1 - 20 #^2 + 80 #^4& , 4, 0]}, {
Root[1 - 40 #^2 + 80 #^4& , 1, 0], Rational[-1, 2], Root[
1 - 20 #^2 + 80 #^4& , 4, 0]}, {
Root[1 - 40 #^2 + 80 #^4& , 1, 0], Rational[1, 2], Root[
1 - 20 #^2 + 80 #^4& , 4, 0]}, {
Root[1 - 40 #^2 + 80 #^4& , 4, 0], Rational[-1, 2], Root[
1 - 20 #^2 + 80 #^4& , 1, 0]}, {
Root[1 - 40 #^2 + 80 #^4& , 4, 0], Rational[1, 2], Root[
1 - 20 #^2 + 80 #^4& , 1, 0]}, {
Root[1 - 20 #^2 + 80 #^4& , 2, 0],
Rational[1, 4] (-1 - 5^Rational[1, 2]), Root[
1 - 20 #^2 + 80 #^4& , 1, 0]}, {
Root[1 - 20 #^2 + 80 #^4& , 2, 0],
Rational[1, 4] (1 + 5^Rational[1, 2]), Root[
1 - 20 #^2 + 80 #^4& , 1, 0]}, {
Root[1 - 20 #^2 + 80 #^4& , 3, 0],
Rational[1, 4] (-1 - 5^Rational[1, 2]), Root[
1 - 20 #^2 + 80 #^4& , 4, 0]}, {
Root[1 - 20 #^2 + 80 #^4& , 3, 0],
Rational[1, 4] (1 + 5^Rational[1, 2]), Root[
1 - 20 #^2 + 80 #^4& , 4, 0]}, {
Root[1 - 290 #^2 + 2555 #^4 - 5850 #^6 + 2025 #^8& , 1, 0],
0, Root[1 - 7720 #^2 + 127280 #^4 - 489600 #^6 + 518400 #^8& ,
6, 0]}, {
Root[1 - 290 #^2 + 2555 #^4 - 5850 #^6 + 2025 #^8& , 8, 0],
0, Root[1 - 7720 #^2 + 127280 #^4 - 489600 #^6 + 518400 #^8& ,
3, 0]}, {
Root[1 - 740 #^2 + 3230 #^4 - 4500 #^6 + 2025 #^8& , 1, 0],
0, Root[1 - 520 #^2 + 40880 #^4 - 835200 #^6 + 518400 #^8& ,
8, 0]}, {
Root[1 - 740 #^2 + 3230 #^4 - 4500 #^6 + 2025 #^8& , 8, 0],
0, Root[1 - 520 #^2 + 40880 #^4 - 835200 #^6 + 518400 #^8& ,
1, 0]}, {
Root[1 - 520 #^2 + 40880 #^4 - 835200 #^6 + 518400 #^8& , 1,
0], Root[1 + 28 # - 20 #^2 - 144 #^3 + 144 #^4& , 4, 0],
Root[
1 - 7720 #^2 + 127280 #^4 - 489600 #^6 + 518400 #^8& , 3,
0]}, {Root[
1 - 520 #^2 + 40880 #^4 - 835200 #^6 + 518400 #^8& , 1, 0],
Root[1 - 28 # - 20 #^2 + 144 #^3 + 144 #^4& , 1, 0], Root[
1 - 7720 #^2 + 127280 #^4 - 489600 #^6 + 518400 #^8& , 3,
0]}, {Root[
1 - 520 #^2 + 40880 #^4 - 835200 #^6 + 518400 #^8& , 8, 0],
Root[1 + 28 # - 20 #^2 - 144 #^3 + 144 #^4& , 4, 0], Root[
1 - 7720 #^2 + 127280 #^4 - 489600 #^6 + 518400 #^8& , 6,
0]}, {Root[
1 - 520 #^2 + 40880 #^4 - 835200 #^6 + 518400 #^8& , 8, 0],
Root[1 - 28 # - 20 #^2 + 144 #^3 + 144 #^4& , 1, 0], Root[
1 - 7720 #^2 + 127280 #^4 - 489600 #^6 + 518400 #^8& , 6,
0]}, {Root[
1 - 7720 #^2 + 127280 #^4 - 489600 #^6 + 518400 #^8& , 3,
0], Root[1 + 28 # - 20 #^2 - 144 #^3 + 144 #^4& , 4, 0],
Root[1 - 520 #^2 + 40880 #^4 - 835200 #^6 + 518400 #^8& , 8,
0]}, {Root[
1 - 7720 #^2 + 127280 #^4 - 489600 #^6 + 518400 #^8& , 3,
0], Root[1 - 28 # - 20 #^2 + 144 #^3 + 144 #^4& , 1, 0],
Root[
1 - 520 #^2 + 40880 #^4 - 835200 #^6 + 518400 #^8& , 8,
0]}, {Root[
1 - 7720 #^2 + 127280 #^4 - 489600 #^6 + 518400 #^8& , 6,
0], Root[1 + 28 # - 20 #^2 - 144 #^3 + 144 #^4& , 4, 0],
Root[1 - 520 #^2 + 40880 #^4 - 835200 #^6 + 518400 #^8& , 1,
0]}, {Root[
1 - 7720 #^2 + 127280 #^4 - 489600 #^6 + 518400 #^8& , 6,
0], Root[1 - 28 # - 20 #^2 + 144 #^3 + 144 #^4& , 1, 0],
Root[1 - 520 #^2 + 40880 #^4 - 835200 #^6 + 518400 #^8& , 1,
0]}, {Root[
1 - 1160 #^2 + 40880 #^4 - 374400 #^6 + 518400 #^8& , 1, 0],
Root[1 + 44 # - 100 #^2 - 48 #^3 + 144 #^4& , 3, 0], Root[
1 - 520 #^2 + 40880 #^4 - 835200 #^6 + 518400 #^8& , 1,
0]}, {Root[
1 - 1160 #^2 + 40880 #^4 - 374400 #^6 + 518400 #^8& , 1, 0],
Root[1 - 44 # - 100 #^2 + 48 #^3 + 144 #^4& , 2, 0], Root[
1 - 520 #^2 + 40880 #^4 - 835200 #^6 + 518400 #^8& , 1,
0]}, {Root[
1 - 1160 #^2 + 40880 #^4 - 374400 #^6 + 518400 #^8& , 8, 0],
Root[1 + 44 # - 100 #^2 - 48 #^3 + 144 #^4& , 3, 0], Root[
1 - 520 #^2 + 40880 #^4 - 835200 #^6 + 518400 #^8& , 8,
0]}, {Root[
1 - 1160 #^2 + 40880 #^4 - 374400 #^6 + 518400 #^8& , 8, 0],
Root[1 - 44 # - 100 #^2 + 48 #^3 + 144 #^4& , 2, 0], Root[
1 - 520 #^2 + 40880 #^4 - 835200 #^6 + 518400 #^8& , 8,
0]}, {Root[
1 - 2960 #^2 + 51680 #^4 - 288000 #^6 + 518400 #^8& , 1, 0],
Root[1 + 16 # - 40 #^2 - 192 #^3 + 144 #^4& , 4, 0], Root[
1 - 7720 #^2 + 127280 #^4 - 489600 #^6 + 518400 #^8& , 6,
0]}, {Root[
1 - 2960 #^2 + 51680 #^4 - 288000 #^6 + 518400 #^8& , 1, 0],
Root[1 - 16 # - 40 #^2 + 192 #^3 + 144 #^4& , 1, 0], Root[
1 - 7720 #^2 + 127280 #^4 - 489600 #^6 + 518400 #^8& , 6,
0]}, {Root[
1 - 2960 #^2 + 51680 #^4 - 288000 #^6 + 518400 #^8& , 8, 0],
Root[1 + 16 # - 40 #^2 - 192 #^3 + 144 #^4& , 4, 0], Root[
1 - 7720 #^2 + 127280 #^4 - 489600 #^6 + 518400 #^8& , 3,
0]}, {Root[
1 - 2960 #^2 + 51680 #^4 - 288000 #^6 + 518400 #^8& , 8, 0],
Root[1 - 16 # - 40 #^2 + 192 #^3 + 144 #^4& , 1, 0], Root[
1 - 7720 #^2 + 127280 #^4 - 489600 #^6 + 518400 #^8& , 3,
0]}}, {{0, 0, -0.9510565162951532}, {
0, 0, 0.9510565162951536}, {-0.8506508083520394,
0, -0.4253254041760197}, {
0.85065080835204, 0,
0.42532540417602}, {-0.6881909602355868, -0.5,
0.42532540417602}, {-0.6881909602355868, 0.5,
0.42532540417602}, {
0.6881909602355868, -0.5, -0.4253254041760197}, {
0.6881909602355868,
0.5, -0.4253254041760197}, {-0.2628655560595671, \
-0.8090169943749475, -0.4253254041760197}, {-0.2628655560595671,
0.8090169943749475, -0.4253254041760197}, {
0.2628655560595668, -0.8090169943749475, 0.42532540417602}, {
0.2628655560595668, 0.8090169943749475,
0.42532540417602}, {-1.5443455162844653`, 0,
0.29494374842358073`}, {
1.5443455162844655`,
0, -0.29494374842358073`}, {-0.9544580194373125, 0,
1.2494017678608846`}, {
0.954458019437308,
0, -1.2494017678608846`}, {-1.2494017678608846`,
0.9077435189160142, -0.29494374842358073`}, \
{-1.2494017678608846`, -0.9077435189160141, -0.29494374842358073`}, {
1.2494017678608846`, 0.9077435189160142,
0.29494374842358073`}, {
1.2494017678608846`, -0.9077435189160141,
0.29494374842358073`}, {-0.29494374842358073`,
0.9077435189160142,
1.2494017678608846`}, {-0.29494374842358073`, \
-0.9077435189160141, 1.2494017678608846`}, {0.29494374842358073`,
0.9077435189160142, -1.2494017678608846`}, {
0.29494374842358073`, -0.9077435189160141, \
-1.2494017678608846`}, {-0.7721727581422326,
0.5610163477575296, -1.2494017678608846`}, \
{-0.7721727581422326, -0.5610163477575298, -1.2494017678608846`}, {
0.7721727581422327, 0.5610163477575296,
1.2494017678608846`}, {
0.7721727581422327, -0.5610163477575298,
1.2494017678608846`}, {-0.4772290097186562,
1.468759866673544,
0.29494374842358073`}, {-0.4772290097186562, \
-1.468759866673544, 0.29494374842358073`}, {0.477229009718654,
1.468759866673544, -0.29494374842358073`}, {
0.477229009718654, -1.468759866673544, \
-0.29494374842358073`}}],
Polygon3DBox[{{21, 2, 12}, {21, 12, 6}, {21, 6, 2}, {15, 2,
6}, {15, 6, 5}, {15, 5, 2}, {22, 2, 5}, {22, 5, 11}, {22, 11,
2}, {28, 2, 11}, {28, 11, 4}, {28, 4, 2}, {27, 2, 4}, {27, 4,
12}, {27, 12, 2}, {24, 7, 9}, {24, 9, 1}, {24, 1, 7}, {16, 8,
7}, {16, 7, 1}, {16, 1, 8}, {23, 10, 8}, {23, 8, 1}, {23, 1,
10}, {25, 3, 10}, {25, 10, 1}, {25, 1, 3}, {26, 9, 3}, {26, 3,
1}, {26, 1, 9}, {29, 12, 10}, {29, 10, 6}, {29, 6, 12}, {13,
6, 3}, {13, 3, 5}, {13, 5, 6}, {30, 5, 9}, {30, 9, 11}, {30,
11, 5}, {20, 11, 7}, {20, 7, 4}, {20, 4, 11}, {19, 4, 8}, {19,
8, 12}, {19, 12, 4}, {32, 7, 11}, {32, 11, 9}, {32, 9, 7}, {
14, 8, 4}, {14, 4, 7}, {14, 7, 8}, {31, 10, 12}, {31, 12,
8}, {31, 8, 10}, {17, 3, 6}, {17, 6, 10}, {17, 10, 3}, {18, 9,
5}, {18, 5, 3}, {18, 3, 9}}]]},
ImageSize->{49., Automatic}]\)^10 - 1)]