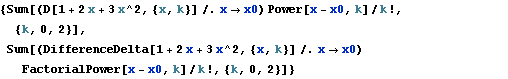Provide FactorialPower as a Basis for Discrete Calculus

New in Wolfram Mathematica 7: New Categories of Special Functions

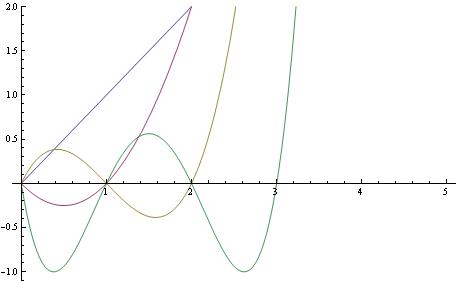
FactorialPower plays the same role in discrete calculus that Power does in continuous calculus, including simple derivatives and intetegrals and the basis for a standard series representation.

In[1]:=

{D[Power[x, n], x], 

  DifferenceDelta[FactorialPower[x, n], x]} // TraditionalForm

Out[1]//TraditionalForm=

In[2]:=

{Integrate[Power[x, n], x], 

  Sum[FactorialPower[x, n], x]} // TraditionalForm

Out[2]//TraditionalForm=

In[3]:=

{Sum[(D[1 + 2 x + 3 x^2, {x, k}] /. x -> x0) Power[x - x0, k]/k!, {k, 

   0, 2}],

 Sum[(DifferenceDelta[1 + 2 x + 3 x^2, {x, k}] /. 

     x -> x0) FactorialPower[x - x0, k]/k!, {k, 0, 2}]}

Out[3]=

In[4]:=

{Sum[(D[1 + 2 x + 3 x^2, {x, k}] /. x -> x0) Power[x - x0, k]/k!, {k, 

   0, 2}],

 Sum[(DifferenceDelta[1 + 2 x + 3 x^2, {x, k}] /. 

     x -> x0) FactorialPower[x - x0, k]/k!, {k, 0, 2}]};

First[%] - Last[%] // FunctionExpand // Expand

Out[4]=

In[5]:=

Plot[Evaluate@Table[FactorialPower[x, k], {k, 1, 4}], {x, 0, 5}, 

 PlotRange -> {-1.1, 2}]

Out[5]=