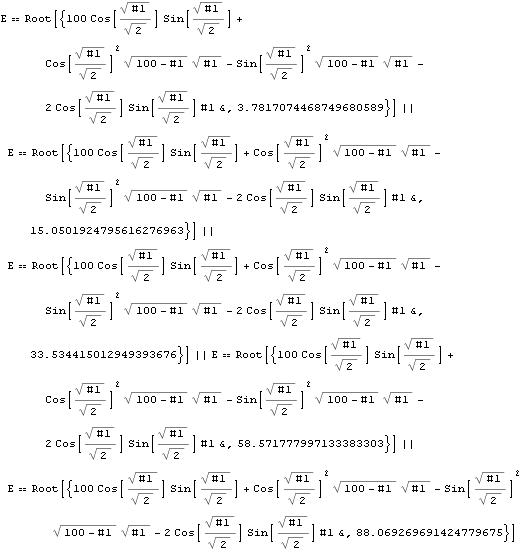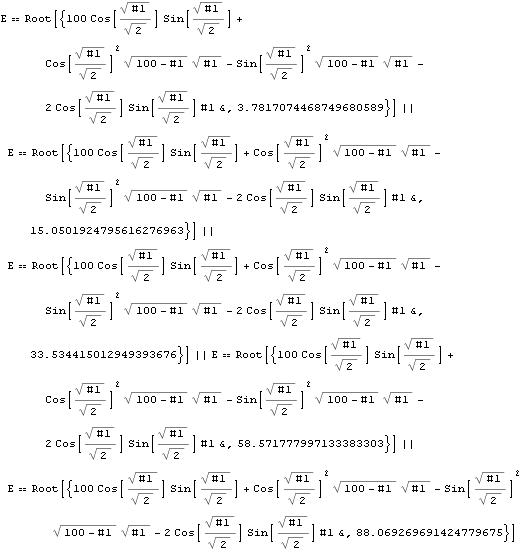Find the Energy Spectrum for a Finite Potential Well

New in Wolfram Mathematica 7: Transcendental Roots

◄ previous | next ►

Find the energy spectrum for particles of mass m in a potential well of width L and height

Show the solutions normalized to be 1 at

In[1]:=

\[Alpha] = Sqrt[

 2 m (\[CapitalGamma] - \[CapitalEpsilon])]/\[HBar]; k = Sqrt[

 2 m \[CapitalEpsilon]]/\[HBar];

Subscript[\[Psi], 1] = G Exp[\[Alpha] x]; Subscript[\[Psi], 2] = 

 A Sin[k x] + B Cos[k x]; Subscript[\[Psi], 3] = H Exp[-\[Alpha] x];

bconds = {(Subscript[\[Psi], 1] /. x -> -L/2) == (Subscript[\[Psi], 

      2] /. x -> -L/2), (Subscript[\[Psi], 2] /. 

      x -> L/2) == (Subscript[\[Psi], 3] /. x -> L/2), (\!\(

\*SubscriptBox[\(\[PartialD]\), \(x\)]

\*SubscriptBox[\(\[Psi]\), \(1\)]\) /. x -> -L/2) == (\!\(

\*SubscriptBox[\(\[PartialD]\), \(x\)]

\*SubscriptBox[\(\[Psi]\), \(2\)]\) /. x -> -L/2), (\!\(

\*SubscriptBox[\(\[PartialD]\), \(x\)]

\*SubscriptBox[\(\[Psi]\), \(2\)]\) /. x -> L/2) == (\!\(

\*SubscriptBox[\(\[PartialD]\), \(x\)]

\*SubscriptBox[\(\[Psi]\), \(3\)]\) /. x -> L/2)};

d = Det[CoefficientArrays[bconds, {A, B, G, H}][[2]]];

\[HBar] = 1; L = 1; \[CapitalGamma] = 100; m = 1;

spec = Reduce[d == 0 && \[CapitalEpsilon] > 1/1000, \[CapitalEpsilon],

   Reals]

Out[1]=

In[2]:=

sols = (Piecewise[{{Subscript[\[Psi], 1], 

           x < -L/2}, {Subscript[\[Psi], 2], -L/2 < x < L/2}}, 

         Subscript[\[Psi], 3]] /. # /. 

       Solve[bconds /. #, {A, B, G}] /. 

      H -> (Exp[

          Sqrt[(\[CapitalGamma] - \[CapitalEpsilon])/2]] /. #)) & /@ 

   N[{ToRules[spec]}, 20];

In[3]:=

Plot[sols, {x, -2, 2}, PlotRange -> All]

Out[3]=