The Wolfram Solution forControl SystemsBuild and analyze control systems, document design decisions, and interactively evaluate controllers–all in one system, with one integrated workflow. Underlying the Wolfram control systems solution is a powerful hybrid symbolic-numeric computation engine with numerics of any precision, high-performance symbolics, advanced visualizations, and automated algorithm selection–everything to get accurate results efficiently. The Wolfram solution is ideal for testing ideas and designing efficient and reliable control systems. |
 |
Wolfram technologies include thousands of built-in functions that let you:
- Compute the state-space model of a system described by difference or differential equations and any algebraic constraints
- Analyze the stability of a system using built-in frequency-response tools, computing the poles, or solving a Lyapunov equation
- Simplify models of systems with interconnected components using block-diagram reduction
- Manipulate linear models as transfer-function or state-space data objects
- Interactively analyze the system behavior as parameters are varied
- Employ classical techniques such as Bode, Nyquist, Nichols, and root locus plots to analyze and design control systems
- Evaluate the controllability and observability properties of a system
- Compute state-space transformations to obtain decompositions that are controllable, observable, minimal, or balanced
- Obtain continuous-time equivalents of discrete-time systems for analysis and design
- Develop feedback laws to enhance the performance of dynamic systems
- Design and analyze systems with time delays and algebraic equations
- Automatically compute design quantities including closed-loop transfer functions, PID parametrizations, and more
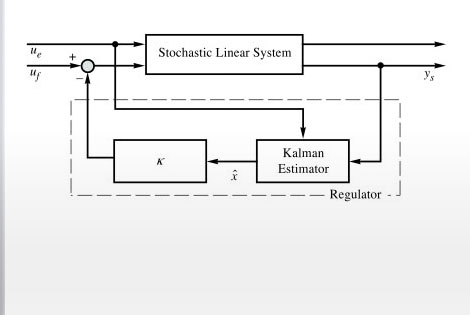
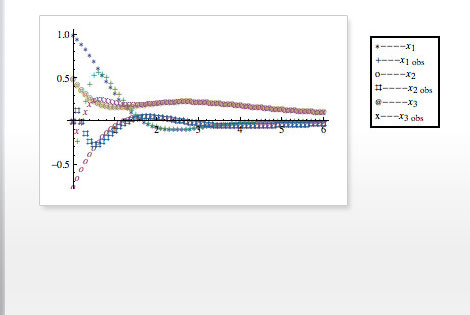
- Estimate unmeasured states or noisy measurements
- Directly obtain models of controllers and estimators that can be easily assembled to form a closed-loop system for further simulations
- Discretize continuous-time feedback algorithms for real-time implementation
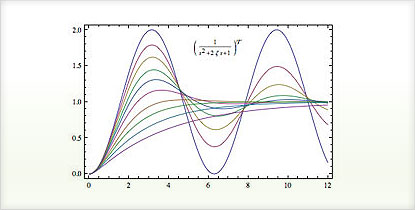
Simulating the response of state-space or transfer-function models
Determining system stability using built-in functions
Does your current tool set have these advantages?
-
Directly input both transfer-function and state-space models in natural form
Matlab allows you to specify transfer-function models only as a matrix of row vectors -
Analyze symbolic and numeric systems
Matlab handles numeric systems only -
Fully automated precision control and arbitrary precision arithmetic to ensure accurate results
Matlab and other systems relying on machine arithmetic can show critical errors due to numerical accuracy failure -
Instant interface construction to test a control system interactively for different scenarios
Unique to Wolfram technologies -
Free-form linguistic input produces immediate results without the need for syntax
Unique to Wolfram technologies -
Automated algorithm selection to get accurate results quickly—sometimes switching mid-calculation for further optimization
Other computation systems like Matlab make you analyze your equations manually to determine which function to apply -
Control systems functionality is well integrated with the core Wolfram Language and more than 20 built-in application areas, such as
signal processing, time series, image processing, wavelets, linear algebra, and more
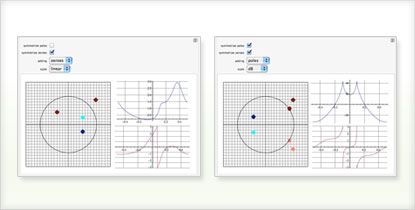
Building a transfer function out of a collection of poles and zeros in the complex plane
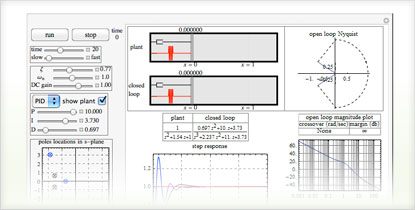
Simulating a feedback control system with controller and second-order plant
Control systems specific capabilities:
- Specify state-space and transfer-function models in natural form, and easily convert from one form to another
- Obtain linearized state-space models of systems described by differential or difference equations and any algebraic constraints
- Freely convert between continuous-time and discrete-time models using a wide selection of algorithms
- Perform system manipulations, such as selecting or deleting subparts, cascading a set of systems, constructing interconnections of subsystems, and more
- Analyze and design systems using frequency-response tools centered around Bode plot, Nyquist plot, Nichols plot, and singular-value plot
- Analyze state-space models and convert between different realizations, including Kalman, Jordan, balanced, and other forms
- Integrated functionality for designing and analyzing control systems including models with time delays and algebraic equations »
- Automatic tuning of PID controllers »
- Improve the performance of systems using a broad selection of feedback design tools such as robust pole-assignment algorithms and linear-quadratic optimal control methods
- Simulate open- and closed-loop systems to determine state and output responses
- Analyze a control system interactively for different scenarios using the Manipulate command »
- Solve Riccati and Lyapunov equations using built-in functions
- Connect to databases instantly for easy access to specialized data
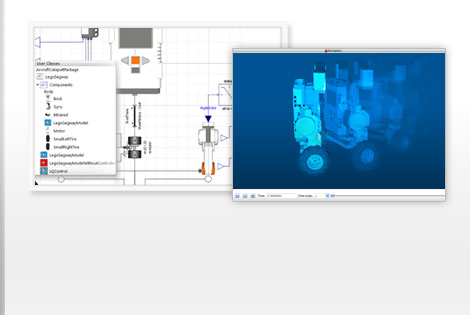
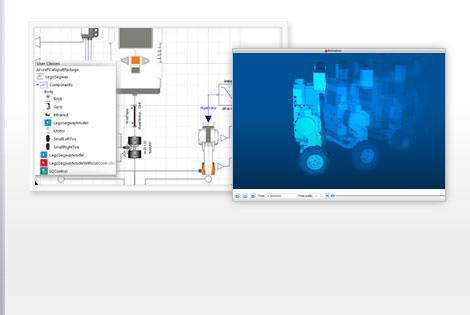
Wolfram SystemModeler is the most complete physical modeling and simulation tool for high-fidelity modeling. With SystemModeler, you can:
- Build models of complex, multi-domain systems using simple drag-and-drop of ready-made components; derive the state-space representations; and evaluate the models »
- Design and simulate real-world systems that exhibit rapid changes or discontinuities »
- Connect seamlessly with Mathematica for the ultimate integrated modeling, simulation, and analysis workflow
Download a Free Trial
Get your free, fully functional, 15-day trial version of Mathematica and SystemModeler via download.
|
|