Wolframソリューション高性能計算高性能計算では,最も難しい技術的な問題に対して正しい答を返すことが求められます.このような問題は非常に複雑であるため,多くのシステムは現実的な計算時間や信頼性できる結果を提供することができません. Wolframテクノロジーはこの両方を提供します.重要な高性能計算(HPC)の技術が単一のシームレスなシステムに統合されているため,ユーザはスピードと確度のどちらかを選ばなくてはならないということがありません.Wolframは,これらの技術の多くを自動化された形で適用し,正確な答を素早く提供することができる高性能計算環境を提供します. |
 |
Wolframの強み
Wolframを使う理由
主な機能
Wolframテクノロジーには次のような何千もの組込み関数が含まれています
- 計算機能,性能,高速開発機能をユニークに組み合せるWolfram言語を使って,大規模な生産システムを構築
- コードを書く前にアーキテクチャを評価して改良したり,アプリケーションを完全に実装する前にコードの一部の性能をテストしたりする
- コード化のプロセスを自動化することで,完成までの期間を劇的に短縮
- 実行時間をプロットして入力サイズとの対応を見るために,実行時間をプロットする
- CUDAあるいはOpenCLの計算を使って,金融計算や線形代数計算を向上させる
- CUDAアーキテクチャを使って,デブリや流体の物理法則を踏まえたシミュレーションを計算したり,高性能を要求する他の分野のアプリケーションを高速化したりする
- gridMathematicaを使って,コードを変更せずに,ローカルのハードウェア,クラスタ,アドホックグリッドから追加の処理パワーを自動的に利用する
- 古典モンテカルロ法および量子モンテカルロ法を使って,複雑な多体物理系のシミュレーションを行う
- GPUを使ったフィルタリング,モルフォロジ,二項演算のための組込み関数で,強力な画像処理を実行する
- 大規模なシミュレーションを実行して複雑な熱力学系のモデルをテストする
- 大きいゲノムに対してGPUに最適化されたBLAST検索を実行する
- 他では不可能な,長さと時間のスケール上でのタンパク質の動力学研究
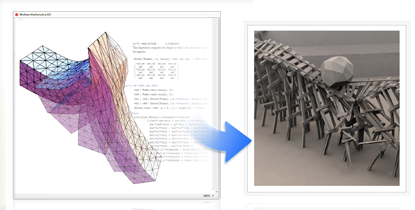
この物理シミュレーションエンジンのような大規模の製造システムを構築するのに,高性能計算に依存する
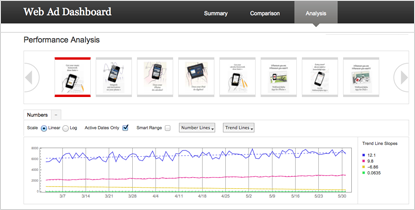
卓越したユーザ体験と開発の柔軟性を備えた,計算量の多いビジネスインテリジェンスアプリケーションを開発する
Wolframの強み
Wolframを使う理由
主な機能
現在お使いのツールには以下のような利点がありますか.
- 数学,科学,工学の多岐に渡る,業界で最大の組込みアルゴリズムコレクションを基盤として,少ないコードで,他のプラットフォームでは不可能なタスクを成し遂げる
- コードを書き進めながら,その一部ををテストすることが,コンパイルされた言語よりも簡単にできる
- gridMathematicaを介して,クラスタ管理システムを含むHPC標準を幅広くサポート
- Wolfram言語側での設定を必要としない組込みのマルチコア,マルチCPU,GPUの並列化機能
- 並列カーネルの状態,負荷分散,並行モニタリング等の並列処理メトリックを動的に表示
- 包括的で使いやすい高レベルのインターフェースによって,完全にスケーラブルなCUDAおよびOpenCLのプログラムを構築してロードする
- 高度に自動化された機械学習関数が,広範に渡る複雑な計算タスクへの即時アクセスを提供
- Wolfram言語式に対する組込みのシリアル化機能で,システムの状態を保存・復元することが簡単に
- 他の言語で必要なコードのわずか数分の一の量で,作業が遂行できる
- プログラムに関連したコード,ドキュメント,テストケース,例題,計算を非常に整理しやすい1つのドキュメントの中に混在させる
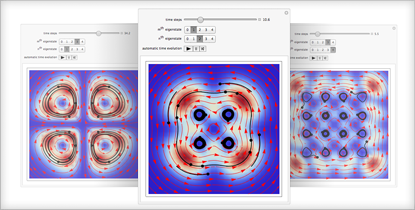
複雑な量子シミュレーションを実行し,リアルタイムで操作する
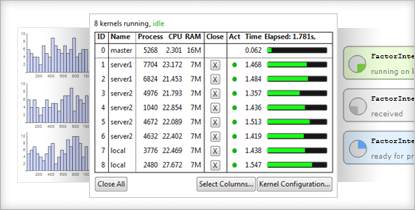
組込み関数を使って,並列処理マトリクスを表示する
Wolframの強み
Wolframを使う理由
主な機能
Wolfram言語には,計算,モデル作成,可視化,開発,配備のための何千もの組込み関数が含まれています. »
高性能計算に特有の機能:
- すべてのデータ,関数,インターフェースにおいて一貫した記号的なシンタックスと意味を持つ,高レベルの動的言語 »
- 1行からなる高機能のプログラムから,何百万行ものコードを含む大規模プロジェクトまで,どのような規模の開発も可能
- Wolfram Data Dropを使って,デバイス,センサ,プログラム,人等からデータをインポートし統合する »
- スピード,メモリ使用量,ロバスト性について最適化された,世界最大のアルゴリズム網 »
- Wolfram言語のタスク指向のスーパー関数が,指定された使い方に最適なアルゴリズムを自動的,動的に選択
- 高度な機械学習関数が,予測解析,自動前処理,複雑なデータ分類のための時間節約ツールを提供 »
- コアとなるルーチンが特定のハードウェアに最適化されているが,ベンダーが最適化したライブラリの方がよい場合はそちらを使う
- CUDAおよびOpenCLの計算に対する高レベルのサポートで,利用可能なハードウェアを十分に活用する »
- 線形代数,画像処理,金融シミュレーション,フーリエ変換等の分野のための,GPUで強化された組込み関数
- ローカルのマルチコアあるいはマルチCPUハードウェアを自動的に使用したり,複数のCPU/GPUをローカルやリモートで実行したり,gridMathematicaを使って複数のグリッド間で使ったりする »
- 64ビットの完全実装によって,より大きなメモリにアクセスでき,ハードウェアがより効率的に利用できる