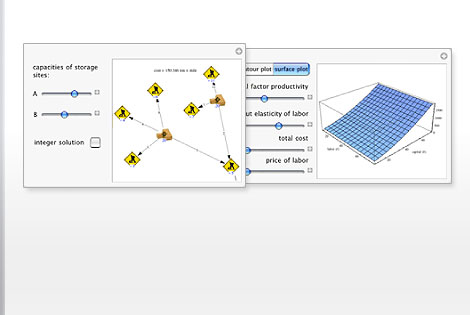
Wolframソリューションオペレーションズリサーチ強力な計算，分析，動的なレポート生成を利用して，配備が簡単で完全にインタラクティブなモデルでプロセスのシミュレーションを行います．これらの作業すべてが単一のシステムの中で，統合されたワークフローで行えます． Wolframのオペレーションズリサーチのソリューションの基礎となっているのは，最先端の局所的・大域的最適化技術，高度なグラフアルゴリズム，効率的な乱数生成です． |
 |
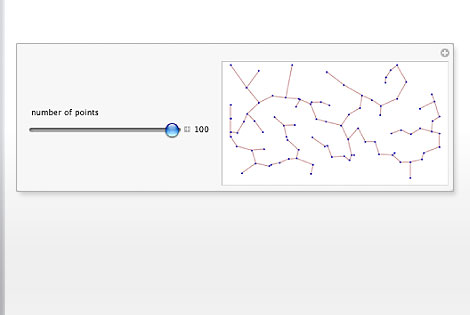
Wolframの強み
Wolframを使う理由
主な機能
Wolframテクノロジーには多数の分野についての何千もの組込み関数と精選されたデータが含まれています．
- サプライチェーンのモデル化と最適化
- 工場内での物の流れを効率化する工場レイアウトを設計する
- 動的な車両配分問題を解く
- 区間ベースおよびネットワークベースの座席リストの管理を行って，航空会社の収益を最大化する
- 船舶の航路決定，スケジューリング，船隊の利用等の海洋輸送業務を最適化する
- 航空機と乗務員のスケジュール設定，および空港，航空交通等の航空インフラストラクチャ業務を行う
- 病院における外来患者の待ち時間を最小化したり，マテリアルハンドリングシステムにおける待ち行列ネットワークを探究したりするためのコンピュータシミュレーションを開発する
- 待ち行列システムを分析し，マルコフ(Markov)過程の計算を実行する
- クリティカルパス分析あるいはPERT法を使った効率的なプロジェクト管理を遂行する
- システムの信頼性を向上させる
- 機械組立品や生物系の寿命を推定する
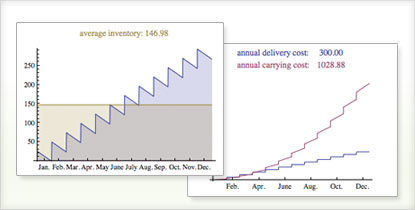
定期配送を受けている事業所の在庫規模と在庫費用をモデル化する
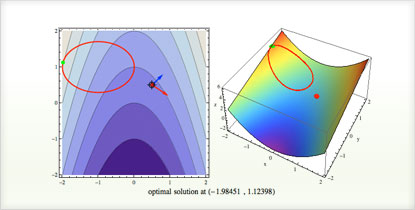
ある制約条件における関数の最小化と最大化を描写する
Wolframの強み
Wolframを使う理由
主な機能
現在お使いのツールには以下のような利点がありますか．
-
シミュレーションの可視化を行ったり，パラメータの変更に対するモデル感度を調べたりするために，インタラクティブなインターフェースを自動構築する
Wolframテクノロジー特有の機能 -
RandomReal，RandomInteger，RandomComplexといった組込み関数を使って，確率過程，離散事象等のコンピュータシミュレーションを簡単に開発する
C/C++，Java，およびその他のプログラミング言語では，連続分布と離散分布から乱数生成を行うために，ライブラリをインポートし，非常に長いコードを書く必要がある -
自動精度制御と任意精度数値計算が，条件の悪い問題について高度に正確な結果を生成する
Excel，Matlab，および有限精度の数値計算に依存するその他のシステムでは，精度の不足により，クリティカルエラーを起す可能性がある -
制約条件付き，および制約条件なしの最適化，統計の解析と計算，曲線のフィット，およびその他の広範に渡る適用分野のための，組込みの機能
Matlabでは複数のツールボックスを購入する必要がある -
計算量あるいはデータ量の多い問題を解くために，マルチコアのコンピュータやグリッドで簡単に使える並列計算機能
他のすべてのシステムにおいては，処理を並列化するのに大々的なプログラミングを行うことが必要 -
計算に即座に適用できる，過去と現在の金融，社会経済，地理，科学のデータへの統合されたアクセス
Wolframテクノロジー特有の機能 -
シミュレーションから分析，タイプセットしたドキュメントやインタラクティブなスライドショーまで，単一のドキュメントで行える完全なワークフロー
Wolframテクノロジー特有の機能
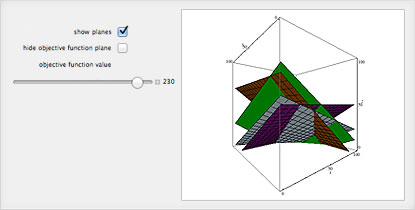
線形計画問題の解をグラフィックスで求める
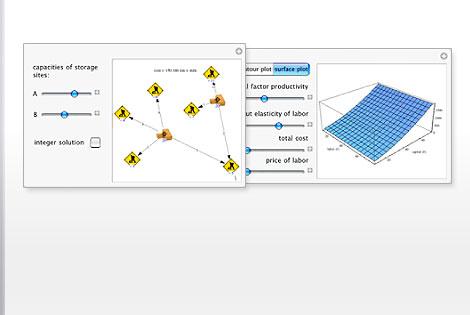
ライフサイクルが短い製品のキャパシティプランニング
Wolframの強み
Wolframを使う理由
主な機能
Wolframテクノロジーには，計算，モデル作成，可視化，開発，配備のための何千もの組込み関数が含まれています． »
オペレーションズリサーチに特有の機能：
- 組込みの生存解析機能を使って，機械組立品や生物系の寿命を推定する »
- システムの信頼性を向上させるのに役立つサブシステムを特定するための重要性測定を含む，信頼性解析のための完全な機能 »
- インターネット輻輳制御，高速通信ネットワークの設計といったネットワーク経路選定のアプリケーションに使える，ダイクストラ(Dijkstra)，クラスカル(Kruskal)，ベルマン・フォード(Bellman–Ford)等を含む高度なグラフアルゴリズム
- 中心性測定や距離測定等のグラフの測定基準を含む，最先端のネットワーク分析およびグラフ計算の機能 »
- イベントのシミュレーション，確率の推測，記号的結果の数値的な検証等のための効率的な乱数生成 »
- 自由形式の言語入力によって，シンタックスを気にせずに結果を即座に出すことが可能 »
- 即座にインタラクティブなインターフェースを作成し，パラメータの変更に対するモデル感度を調べる »
- 制約条件付きの非線形最適化を含む，局所的・大域的最適化の問題を数値的，および記号的に解くための組込み関数 »
- 微積分，確率，グラフ理論を使った数学モデル構築に対する高レベルのサポート
- 統計解析のための，線形，非線形，ロジット，プロビット，一般化された線形，その他の回帰のモデル »
- データからの分布母数の推定および分布に対するデータの適合度の検定
- 新しい分布をデータ，式，あるいは別の分布から定義する機能を持つ統計分布を他のどのシステムよりも多く持つ »
- 自由形式の言語入力，変換，グラフィックスや数値・記号計算全般の次元一致チェックを含む，4500を超える単位の組込みサポート »
- パラメトリック過程，有限マルコフ過程，待ち行列過程，時系列過程，確率微分方程式過程を含む，ランダム過程の幅広いサポート
- 離散時間および連続時間の有限マルコフ過程のサポート，および一般的な到着分布とサービス時間分布に従う有限および無限の待ち行列と待ち行列ネットワークのサポート
- シンプレックス法，改訂シンプレックス法，内点法のいずれかを使って線形計画問題を解く
- 自動アルゴリズム選択，あるいは焼きなまし法，Nelder-Mead法，微分進化法，ランダム探索法等のユーザ指定の方法を使った多次元の最適化問題解法 »
- 高速でメモリ効率のよい実行を行うための，並列処理およびCUDAあるいはOpenCLを使ったGPU計算への組込みサポート
- グラフィックス，テキスト，インタラクティブアプリケーションを含む動的なレポートを生成する »
- Wolfram CDF Player やwebMathematica を使って，インタラクティブなモデルを即時配備する
Wolframテクノロジーを使用している機関の例
 |
 |
 |
 |
Mathematica 無料評価版のダウンロード
完全な機能を備えた Mathematica の無料評価版（15日間有効）がダウンロードで入手できます．
|
