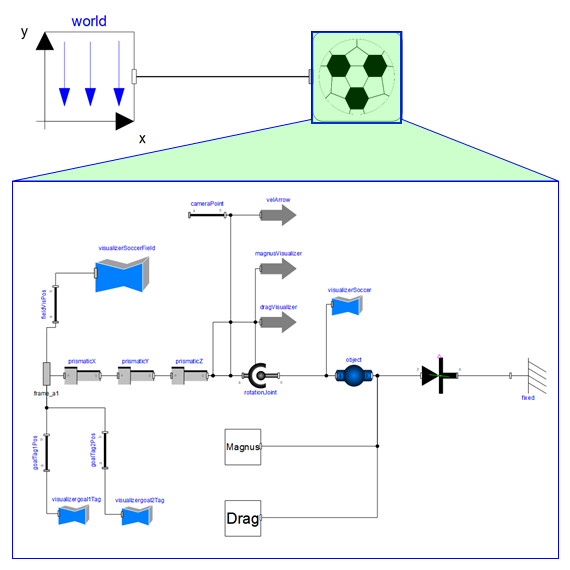
Patee como Beckham
¿Alguna vez se ha preguntado cómo Roberto Carlos o David Beckham podían engañar a los porteros dándole efecto al balón? Quizás no, ya que son tan hábiles, pero ¿se ha preguntado por qué el efecto realmente cambia la trayectoria del balón? Este ejemplo modela un tiro libre en el fútbol y examina lo que ocurre.
Para ejecutar este ejemplo necesitará
Las versiones más recientes de System Modeler y Mathematica.
Por favor haga una selección:
Obtener unaprueba gratuita Continuar
con la descarga
Observe un tiro libre con la fuerza Magnus en acción. Las fuerzas (Magnus: roja, arrastre: verde) y los vectores de velocidad (azul) se muestran en la animación de la simulación.
El modelo
Esencialmente, todo lo que necesita un modelo de tiro libre es un balón que pueda moverse y rotar. La parte complicada es asignar las fuerzas correctas que actúan sobre el balón, dependiendo de la velocidad y el efecto. Tres fuerzas afectan al balón: la gravedad (fuerza hacia abajo), el arrastre (fuerza que se opone al vector de velocidad) y la fuerza Magnus (dependiente de la velocidad, la velocidad angular y el eje de giro).
Vista del diagrama del modelo Free Kick con el componente Ball. Las fuerzas Magnus y de arrastre, así como un elemento de visualización y contacto, están conectadas a un cuerpo para transformarlo en un balón de fútbol.
Fuerza Magnus y fuerza de arrastre
La fuerza Magnus depende del efecto y la velocidad. Todas las demás variables que contribuyen a la fuerza Magnus pueden agruparse en el llamado "coeficiente de sustentación", Cl, el cual es difícil de calcular de forma analítica y, a menudo, se mide experimentalmente. La representación a la izquierda muestra datos experimentales del coeficiente de sustentación frente a la relación de giro (=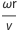 
, velocidad de rotación por radio dividido entre velocidad) y la función utilizada para aproximar Cl. La fuerza de arrastre depende de la velocidad y del número de Reynolds. La representación a la derecha muestra datos experimentales del coeficiente de arrastre comparados con el número de Reynolds, junto con la función aproximada para Cd utilizada en el modelo.
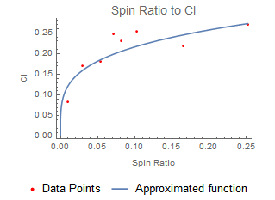
Coeficiente de sustentación para distintas relaciones de giro.
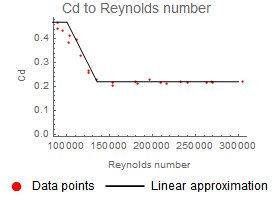
Coeficiente de arrastre para distintos números de Reynolds.
¿Qué velocidad inicial y efecto son necesarios para anotar un gol directamente desde un tiro de esquina?
Las fuerzas (Magnus: roja, arrastre: verde) y los vectores de velocidad (azul) se muestran en la animación de la simulación.
Visualice las fuerzas de manera automática
Dependiendo de la velocidad y el efecto, se calculan las fuerzas y el vector de velocidad cambiará continuamente debido a las fuerzas que actúan sobre el balón.
La velocidad inicial y el efecto necesarios para anotar pueden calcularse analíticamente o, alternativamente (la manera más conveniente), mediante simulaciones para analizar la animación resultante y ajustar los parámetros iniciales. Un ejemplo de condiciones iniciales para anotar desde la esquina es initVel = {35, 8, 12} m/s y initAngVel = {0, 50, 10} rad/s. ¡El video muestra un buen tiro de esquina!
300 tiros de esquina a la vez
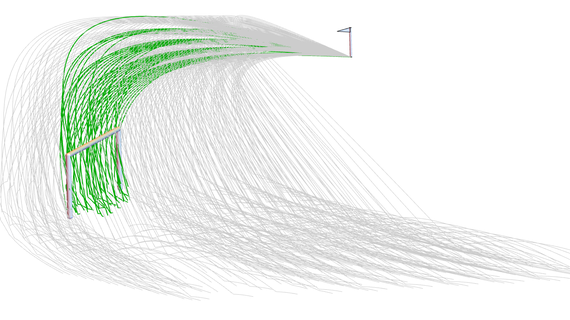
Trayectorias de 300 tiros de esquina con distintas velocidades iniciales. Las trayectorias grises son fallos y las verdes son goles.
Si simular un tiro a la vez le resulta demasiado lento, Mathematica puede ayudar utilizando WSMLink y barridos de parámetros. En el gráfico anterior se realizaron 300 simulaciones con distintas velocidades iniciales al mismo tiempo. De las 300 trayectorias, 45 fueron goles y 255 fallos. ¡Imagine si Beckham hubiera tenido acceso a System Modeler y Mathematica en sus mejores años, cómo podría haber optimizado sus tiros libres!
Wolfram System Modeler
Probar
Comprar
System Modeler está disponible en inglés
y japonés
para Windows, macOS y Linux »
¿Preguntas? ¿Comentarios? Contacte a un experto de Wolfram »