Physique
Élargissez le programme scolaire grâce à des expériences passionnantes dans le domaine de la dynamique et découvrez comment la modélisation et la simulation peuvent améliorer et renforcer la compréhension des concepts de physique et de mathématiques.
Joue-la comme Beckham
Vous êtes-vous déjà demandé comment Roberto Carlos ou David Beckham pouvaient tromper les gardiens de but en faisant tourner le ballon ? Peut-être pas, car ils sont vraiment doués. Mais vous êtes-vous déjà demandé pourquoi la rotation modifie réellement la trajectoire du ballon ? Cet exemple modélise un coup franc au football et examine ce qui se passe.
Pour exécuter cet exemple, il vous faut
les dernières versions de System Modeler et Mathematica.
Veuillez choisir :
Obtenirun essai gratuit Continuer
le téléchargement
Regardez un coup franc avec la force de Magnus en action. Les vecteurs de forces (Magnus en rouge, traînée en vert) et de vitesse (en bleu) sont affichés dans l’animation de la simulation.
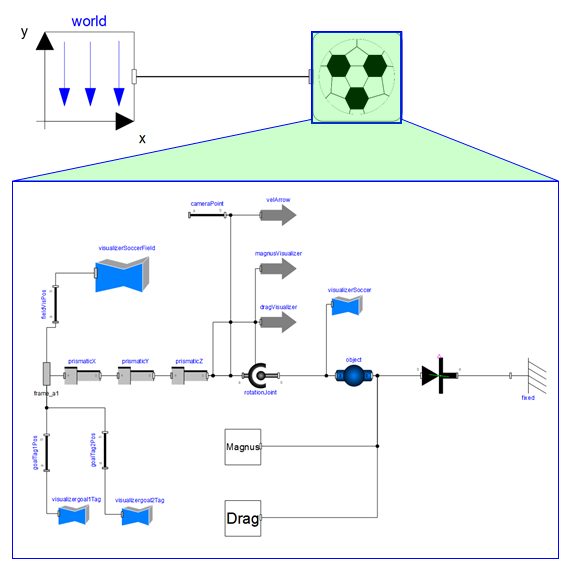
Le modèle
Tout ce dont un modèle de coup franc a besoin, c’est d’un ballon capable de bouger et de tourner. La partie la plus délicate consiste à attribuer les forces appropriées qui agissent sur le ballon, en fonction de la vitesse et de la rotation. Trois forces affectent le ballon : la gravité (force descendante), la traînée (force opposée au vecteur de vitesse) et la force de Magnus (en fonction de la vitesse, de la vitesse angulaire et de l’axe de rotation).
Schéma du modèle de coup franc avec la composante du ballon. Les forces de Magnus et de traînée, ainsi qu’un élément de visualisation et de contact, sont connectées à un corps pour transformer le corps en ballon de football.
Force de Magnus et force de traînée
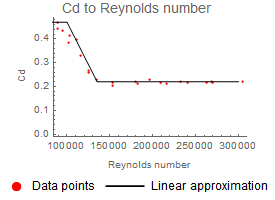
La force de Magnus dépend de la rotation et de la vitesse. Toutes les autres variables contribuant à la force de Magnus peuvent être intégrées dans un « coefficient de portance », Cl. Ce coefficient de portance est difficile à calculer de manière analytique et est souvent mesuré à partir d’expériences. Le tracé de gauche ci-dessous montre les données expérimentales du rapport du coefficient de portance/rotation (=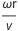 
, vitesse de rotation multipliée par le rayon divisé par la vitesse) et la fonction utilisée pour approximer Cl. La force de traînée dépend de la vitesse et du nombre de Reynolds. Le tracé de droite montre les données expérimentales du coefficient de traînée comparé au nombre de Reynolds, avec la fonction approximative pour Cd utilisée dans le modèle.
Coefficient de portance pour différents rapports de rotation.
Coefficient de traînée pour différents nombres de Reynolds.
Quelle vitesse initiale et quelle rotation sont nécessaires pour marquer un but directement depuis un corner ?
Les vecteurs de forces (Magnus en rouge, traînée en vert) et de vitesse (en bleu) sont représentés dans l’animation de la simulation.
Visualisez les forces automatiquement
En fonction de la vitesse et de l’effet, les forces sont calculées et le vecteur de vitesse changera continuellement en raison des forces agissant sur le ballon.
La vitesse initiale et la rotation nécessaires pour marquer peuvent être calculées de manière analytique ou, alternativement (la manière la plus pratique), être testées en effectuant des simulations et en analysant l’animation obtenue pour voir quel paramètre initial doit être réglé. Un exemple de conditions initiales pour marquer depuis la position du corner est initVel = {35, 8, 12} m/s et initAngVel = {0, 50, 10} rad/s. Regardez la vidéo pour voir un joli tir en corner !
300 tirs en corner en même temps
Trajectoires de 300 tirs en corners avec des vitesses initiales différentes pour chaque coup de pied. Les trajectoires grises correspondent aux tirs ratés et les trajectoires vertes correspondent aux tirs marqués dans les buts.
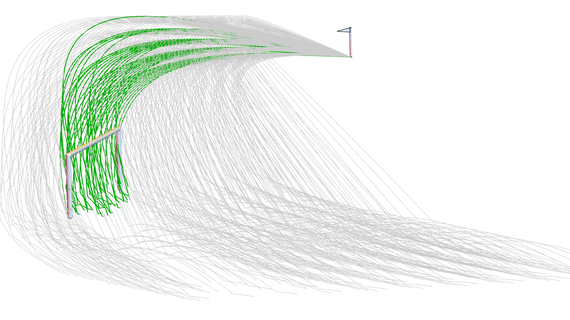
Si vous trouvez que simuler un coup franc à la fois est trop lent, Mathematica peut vous aider en utilisant WSMLink et le balayage des paramètres. Dans le tracé ci-dessus, 300 simulations avec différentes vitesses initiales ont été effectuées en même temps. Sur les 300 trajectoires, 45 buts ont été marqués et 255 ont été ratés. Imaginez si Beckham avait eu accès à System Modeler et Mathematica à l’époque de son apogée, il aurait pu optimiser ses coups francs !
Wolfram System Modeler
Essayez
Achetez
System Modeler est disponible en anglais
et en japonais
sur Windows, macOS et Linux »
Vous avez des questions ou des commentaires ? Contactez un expert Wolfram »