Mersenne Primes and Perfect Numbers
A Mersenne prime is a prime number of the form 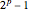 , where the Mersenne prime exponent
, where the Mersenne prime exponent 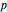 is itself also a prime number. Each Mersenne prime corresponds to an even perfect number.
is itself also a prime number. Each Mersenne prime corresponds to an even perfect number.
Generate a list of Mersenne prime exponents.
In[1]:=
mpe = Table[MersennePrimeExponent[n], {n, 1, 10}]Out[1]=
Construct the corresponding Mersenne primes.
In[2]:=
mp = 2^mpe - 1Out[2]=
Construct the corresponding perfect numbers.
In[3]:=
pn = 2^(mpe - 1) (2^mpe - 1)Out[3]=

In[4]:=
AllTrue[pn, PerfectNumberQ]Out[4]=
Visualize how sparse the distribution of small Mersenne prime exponents is by emphasizing them in red in the list of the first 225 primes.
In[5]:=
primes = Replace[Prime@Range[225],
x_?MersennePrimeExponentQ :> Style[x, Red, Bold], 1];In[6]:=
Multicolumn[primes, Alignment -> {Center, Center}, Spacings -> {1, 1},
Frame -> All, FrameStyle -> Directive[Orange, Dashing[Small]]]Out[6]=