Análise de dados de doenças cardíacas
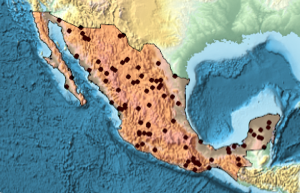
A análise de dados é um processo de extração, apresentação e modelagem com base em informações obtidas em fontes primárias. O exemplo a seguir mostra um fluxo de trabalho de análise de dados na Wolfram Language. O conjunto de dados usado aqui vem do repositório UCI Machine Learning Repository, que consiste em dados de diagnósticos de doenças cardíacas de 1.541 pacientes.
Importe os dados de diagnóstico de doenças cardíacas e analise-os de modo que as linhas correspondam a pacientes diferentes, e as colunas correspondam a atributos diferentes.

rawdata =
Import["https://archive.ics.uci.edu/ml/machine-learning-databases/\
heart-disease/new.data", "Text"];
data = StringSplit[rawdata, LetterCharacter ..];
data = Table[
ToExpression[StringSplit[dat, (" " | "\n") ..]], {dat, data}];Extraia os traibutos relevantes em "marcas" e "propriedades". Os valores armazenados em "marcas" são 0 e 1, os quais correspondem à presença e ausência de doença cardíaca, respectivamente.
labels = Unitize[data[[All, 58]]];
features =
data[[All, {3, 4, 9, 10, 12, 16, 19, 32, 38, 40, 41, 44, 51}]];Take[labels, 10]Para cada paciente, o vetor propriedade é uma lista de valores numéricos. No entanto, os dados não estão completos e possuem campos ausentes armazenados como -9.
features[[-3]]Substitua os valores ausentes pela média dos dados disponíveis no atributo correspondente, em seguida, visualize a correlação entre diferentes atributos.

features = Transpose[Table[
N[attribute /. {-9 -> Mean[N[DeleteCases[attribute, -9]]]}]
, {attribute, Transpose[features]}]];
cormat = Correlation[features];
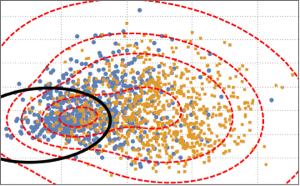
Para visualizar a distribuição dos dados, a PCA é feita para extrair os dois primeiros componentes principais, em seguida, os dados projetados são apresentados em um gráfico de dispersão.
pcs2 = Take[PrincipalComponents[features, Method -> "Correlation"],
All, 2];
Para distinguir as duas classes, os dados projetados são ajustados em um modelo de gaussiano misto de dois componentes.

edist = EstimatedDistribution[pcs2,
MixtureDistribution[{p1,
p2}, {BinormalDistribution[{m11, m12}, {s11, s12}, r1],
BinormalDistribution[{m21, m22}, {s21, s22}, r2]}]];Com base no modelo misto, faça um gráfico dos limites de decisão (curva preta) e contornos de densidade de probabilidade (curva vermelha) do modelo misto, e mostre-os em conjunto com o gráfico de dispersão. O primeiro componente da mistura gaussiana tem maior probabilidade dentro do limite de decisão.