Анализ данных о сердечных заболеваниях

Анализ данных представляет собой процесс извлечения, представления, и моделирования информации, взятой из первоисточников. В этом примере продемонстрирован рабочий процесс выполнения анализа данных с помощью языка программирования Wolfram Language. Данные используемыe в данной демонстрации взяты из базы UCI Machine Learning Repository, которая содержит диагностики болезни сердца 1541 пациентов.

Загрузим данные диагнозов сердечных заболеваний и структурируем их так, чтобы строки соответствовали пациентам, а столбцы - различным симптомам заболеваний.

In[1]:=

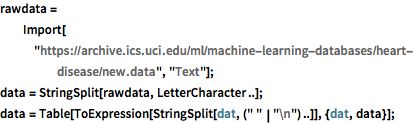
rawdata = Import["https://archive.ics.uci.edu/ml/machine-learning-databases/\ heart-disease/new.data", "Text"]; data = StringSplit[rawdata, LetterCharacter ..]; data = Table[ ToExpression[StringSplit[dat, (" " | "\n") ..]], {dat, data}];

Извлечем характеристики заболеваний и распределим их в переменные "категории" и "особенности". Значения, содержащиеся в "категориях" кодируются как 0 или 1, что соответствуют наличию/отсутствию болезни сердца.

In[2]:=

labels = Unitize[data[[All, 58]]]; features = data[[All, {3, 4, 9, 10, 12, 16, 19, 32, 38, 40, 41, 44, 51}]];

In[3]:=

Take[labels, 10]

Out[3]=

Для каждого пациента, вектор функции представляет собой список числовых значений. Тем не менее, данные не является полными, и пропущенные значения отмечены с помощью -9.

In[4]:=

features[[-3]]

Out[4]=

Заменим пропущенные значения на среднее арифметическое имеющихся данных для соответствующей переменной, а затем визуализируем корреляцию между различными переменными.

In[5]:=

features = Transpose[Table[ N[attribute /. {-9 -> Mean[N[DeleteCases[attribute, -9]]]}] , {attribute, Transpose[features]}]]; cormat = Correlation[features];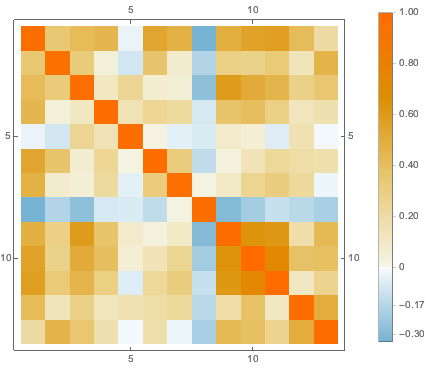

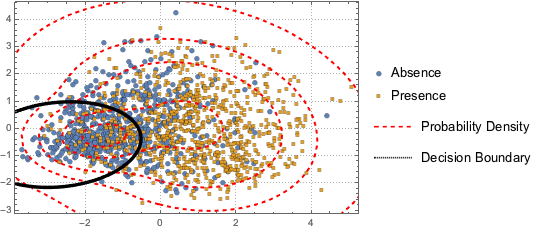
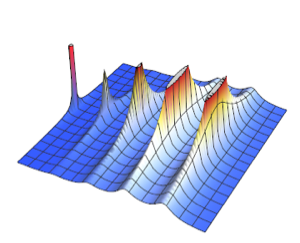
In[6]:=

MatrixPlot[cormat, ImageSize -> Medium, PlotTheme -> "Detailed"]

Out[6]=

Для того, чтобы визуализировать распределение данных, метод главных компонент используется для извлечения первых двух ведущих компонент; далее, проектируемые данные представлены с помощью диаграммы рассеяния.

In[7]:=

pcs2 = Take[PrincipalComponents[features, Method -> "Correlation"], All, 2];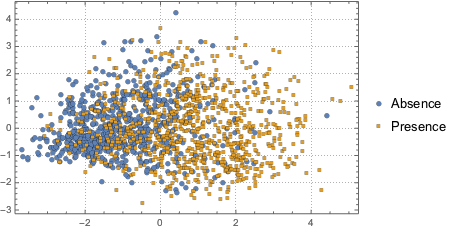

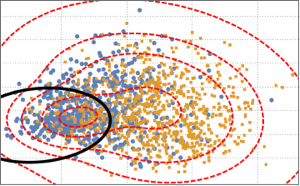
In[8]:=

splot = With[{ind = Pick[Range[Length[pcs2]], labels, 0]}, ListPlot[{pcs2[[ind]], Delete[pcs2, Transpose[{ind}]]}, ImageSize -> Medium, PlotTheme -> "Detailed", PlotMarkers -> Automatic, PlotLegends -> {"Absence", "Presence"}] ]

Out[8]=

Чтобы различать два значения переменной (наличие и отсутствие, см. график), проецируемые данные моделируются на базе двухкомпонентной гауссовой смеси.

In[9]:=

edist = EstimatedDistribution[pcs2, MixtureDistribution[{p1, p2}, {BinormalDistribution[{m11, m12}, {s11, s12}, r1], BinormalDistribution[{m21, m22}, {s21, s22}, r2]}]];

На основе двухкомпонентной гауссовой смеси, обозначим границы решения (черная кривая) и контуры плотности распределения вероятностей (красная кривая) модели смеси и покажем их вместе на диаграмме рассеяния. Первый компонент гауссовой смеси имеет более высокую вероятность внутри границы решения.

In[10]:=

Module[{p = edist[[1, 1]], dist1 = edist[[2, 1]], dist2 = edist[[2, 2]], prob}, prob[x_, y_] := p PDF[dist1, {x, y}]/(p PDF[dist1, {x, y}] + (1 - p) PDF[dist2, {x, y}]); Show[splot, ContourPlot[ PDF[edist, {x, y}] == {0.1, 0.05, 0.0125, 0.003, 0.0001}, {x, -4, 6}, {y, -4, 6}, ImageSize -> Medium, PlotTheme -> "Detailed", ContourStyle -> {Dashed, Thick, Red}, PlotLegends -> LineLegend[{Directive[Red, Dashed]}, {"Probability Density"}], PlotPoints -> 25], ContourPlot[prob[x, y] == 1/2, {x, -4, 6}, {y, -4, 6}, ImageSize -> Medium, PlotTheme -> "Detailed", ContourStyle -> {Thickness[.01], Black}, PlotLegends -> LineLegend[{Directive[Black, AbsoluteDashing[{1, 1}]]}, {"Decision Boundary"}], PlotPoints -> 25]] ]

Out[10]=