Convert Parametric SDE Processes to Equivalent Ito Processes
The canonical form of ItoProcess or StratonovichProcess in Mathematica encodes their defining SDEs 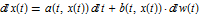 as follows.
as follows.
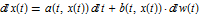 as follows.
as follows. |
WienerProcess solves the SDE 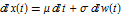 , where
, where 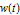 is the standard Wiener process, also known as the Brownian motion process.
is the standard Wiener process, also known as the Brownian motion process.
| In[1]:= | X |
| Out[1]= |
GeometricBrownianMotionProcess solves the SDE 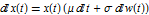 .
.
| In[2]:= | X |
| Out[2]= |
OrnsteinUhlenbeckProcess solves the SDE 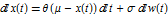 .
.
| In[3]:= | X |
| Out[3]= |
CoxIngersollRossProcess solves the SDE 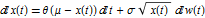 .
.
| In[4]:= | X |
| Out[4]= |
BrownianBridgeProcess solves the SDE 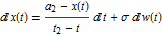 .
.
| In[5]:= | X |
| Out[5]= |