Stochastic Differential Equation for Exponential Decay 

Define a stochastic process satisfying the Ito stochastic differential equation 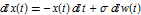. This models exponential decay subject to Wiener noise.

In[1]:=

X \[ScriptCapitalP] = ItoProcess[\[DifferentialD]x[ t] == -x[t] \[DifferentialD]t + \[Sigma] \[DifferentialD]w[t], x[t], {x, x0}, t, w \[Distributed] WienerProcess[]]

Out[1]=

Simulate the process for different values of the variance parameter .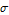

In[2]:=

X Table[ListLinePlot[ RandomFunction[\[ScriptCapitalP] /. {x0 -> 5}, {0, 4, 0.01}, 10], PlotLabel -> Row[{"\[Sigma]", "\[Equal]", N@\[Sigma]}]], {\[Sigma], {1/4, 1/2, 1, 2}}]

Out[2]=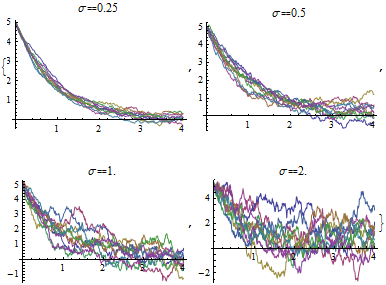

The mean function of the process is independent of .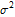

In[3]:=

X Mean[\[ScriptCapitalP][t]]

Out[3]=

This implies that the mean function coincides with the following deterministic solution.

In[4]:=

X x[t] /. DSolve[{x'[t] == -x[t], x[0] == x0}, x[t], t]

Out[4]=

Find the variance function of the process .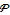

In[5]:=

X Variance[\[ScriptCapitalP][t]]

Out[5]=

Find the probability density function of the value of the process .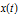

In[6]:=

X PDF[\[ScriptCapitalP][t], x]

Out[6]=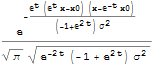