스미스 분해를 사용한 격자 분석
벡터  과
과  의 배수인 정수에 의해 생성된 격자
의 배수인 정수에 의해 생성된 격자  을 검토해 봅니다.
을 검토해 봅니다.
In[1]:=
b1 = {3, -3};
b2 = {2, 1};In[2]:=
ptsb = Flatten[Table[j b1 + k b2, {j, -12, 12}, {k, -12, 12}], 1];In[3]:=
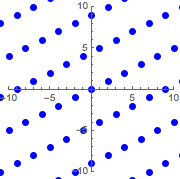
graphicsb =
Graphics[{Blue, PointSize[Large], Point@ptsb}, PlotRange -> 10,
Axes -> True]Out[3]=
 을 행이
을 행이  과
과  의 행렬로 합니다.
의 행렬로 합니다.
In[4]:=
m = {b1, b2};스미스 분해는 항등식  을 만족하는 3개의 행렬을 줍니다.
을 만족하는 3개의 행렬을 줍니다.
In[5]:=
{u, r, v} = SmithDecomposition[m];In[6]:=
u.m.v == rOut[6]=
행렬  와
와  는 정수의 요소와 행렬식 1을 가집니다.
는 정수의 요소와 행렬식 1을 가집니다.
In[7]:=
{u // MatrixForm, v // MatrixForm, Det[u], Det[v]}Out[7]=
행렬  은 정수이며 대각 행렬입니다. 그 항목에서
은 정수이며 대각 행렬입니다. 그 항목에서  의 군의 구조는
의 군의 구조는  또는 간단히
또는 간단히  이며,
이며,  은 자명군입니다.
은 자명군입니다.
In[8]:=
r // MatrixFormOut[8]//MatrixForm=
항등식 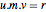 을
을  에 곱하면,
에 곱하면,  이 됩니다.
이 됩니다.  는 정수이며, 행렬식은 1이므로,
는 정수이며, 행렬식은 1이므로,  는
는  과 같은 격자를 생성하지만, 훨씬 간단합니다.
과 같은 격자를 생성하지만, 훨씬 간단합니다.
In[9]:=
g = r.Inverse[v];
g // MatrixFormOut[9]//MatrixForm=
 행에 의해 생성된 격자를 시각화합니다.
행에 의해 생성된 격자를 시각화합니다.
In[10]:=
ptsg = Flatten[
Table[j First[g] + k Last[g], {j, -12, 12}, {k, -12, 12}], 1];In[11]:=
graphicsg =
Graphics[{Red, PointSize[Medium], Point@ptsg}, PlotRange -> 10,
Axes -> True]Out[11]=

새로운 격자를 오리지널 격자에 겹쳐 놓으면 모두 동일한지 확인할 수 있습니다.
In[12]:=
Show[{graphicsb, graphicsg}]Out[12]=