Améliorations dans l'estimation de la distribution

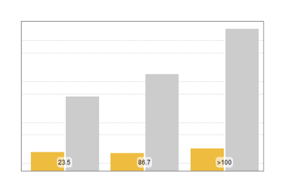
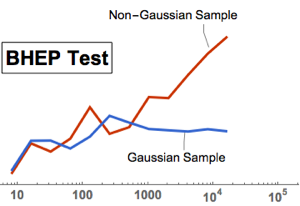
La version 11 ajoute de nombreuses améliorations à l'estimation de la distribution, en particulier dans la performance. Les tableaux suivants montrent les temps pour estimer plusieurs distributions avec différentes tailles d'échantillon. Des expériences ont été effectuées sur un système Windows 10 avec un processeur Intel Xeon E3-1245 v2 3,40 GHz. Le nombre ci-dessous montre que la version 11 est beaucoup plus rapide que la version 10.

Distribution t de Student.

In[1]:=

dist = StudentTDistribution[loc, sc, df]; ndist = StudentTDistribution[-1, 1, 2]; Table[ sample = BlockRandom[SeedRandom["MarketingExample"]; RandomVariate[ndist, n]]; Mean[Table[ First[AbsoluteTiming[EstimatedDistribution[sample, dist];]], {5}]] , {n, {10, 100, 1000}}]

Out[21]=

Distribution de Weibull.

In[2]:=

dist = WeibullDistribution[al, be]; ndist = WeibullDistribution[3, 2]; Table[ sample = BlockRandom[SeedRandom["MarketingExample"]; RandomVariate[ndist, n]]; Mean[Table[ First[AbsoluteTiming[EstimatedDistribution[sample, dist];]], {5}]] , {n, {10, 100, 1000}}]

Out[23]=

Mélange de distributions binormales.

In[3]:=

dist = MixtureDistribution[{w1, w2}, {BinormalDistribution[{m11, m12}, {s11, s12}, \[Rho]1], BinormalDistribution[{m21, m22}, {s21, s22}, \[Rho]2]}]; ndist = MixtureDistribution[{0.3, 0.7}, {BinormalDistribution[{0, 1}, {0.5, 0.25}, 0.7], BinormalDistribution[{-0.5, 0}, {0.5, 0.25}, 0.1]}]; Table[ sample = BlockRandom[SeedRandom["MarketingExample"]; RandomVariate[ndist, n]]; Mean[Table[ First[AbsoluteTiming[ TimeConstrained[EstimatedDistribution[sample, dist];, 100]]], {5}]] , {n, {10, 100, 1000}}]

Out[117]=

Distribution t multivariée.

In[4]:=

dist = MultivariateTDistribution[{{m11, m12}, {m21, m22}}, n]; ndist = MultivariateTDistribution[{{1, 1/3}, {1/3, 1}}, 10]; Table[ sample = BlockRandom[SeedRandom["MarketingExample"]; RandomVariate[ndist, n]]; Mean[Table[ First[AbsoluteTiming[EstimatedDistribution[sample, dist];]], {5}]] , {n, {10, 100, 1000}}]

Out[27]=