Faster Computation of Distribution Properties

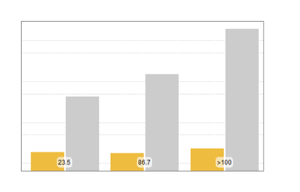
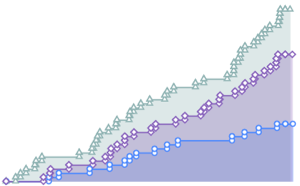
Version 11 enhances the numerical computation of a wide variety of distribution properties. The following charts show the speed comparisons for different sample sizes. Experiments were performed on a Windows 10 system with an Intel Xeon Processor E3-1245 v2 3.40 GHz. The number at the bottom shows how much faster Version 11 is than Version 10.

Better listability support for PDF.

In[1]:=

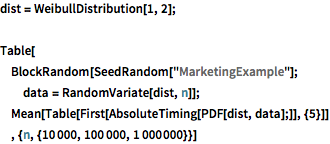
dist = WeibullDistribution[1, 2]; Table[ BlockRandom[SeedRandom["MarketingExample"]; data = RandomVariate[dist, n]]; Mean[Table[First[AbsoluteTiming[PDF[dist, data];]], {5}]] , {n, {10000, 100000, 1000000}}]

Out[168]=

Faster quantile for discrete distributions.

In[2]:=

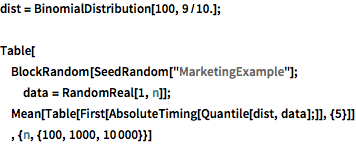
dist = BinomialDistribution[100, 9/10.]; Table[ BlockRandom[SeedRandom["MarketingExample"]; data = RandomReal[1, n]]; Mean[Table[First[AbsoluteTiming[Quantile[dist, data];]], {5}]] , {n, {100, 1000, 10000}}]

Out[170]=

Probability of a multivariate hypergeometric distribution.

In[3]:=

Table[ Mean[Table[First[AbsoluteTiming[TimeConstrained[ BlockRandom[SeedRandom["MarketingExample"]; symbols = Table[Unique[a], {n}]; Probability[Min[symbols] >= 2 && Max[symbols] <= 12, symbols \[Distributed] MultivariateHypergeometricDistribution[30, RandomInteger[{20, 40}, n]]]; ], 100]]], {5}]], {n, {2, 3, 4}}]

Out[30]=