Sample from a Poisson Point Process

A Poisson point process is a generalization of the one-dimensional Poisson process to a multidimensional case. A homogeneous Poisson point process in geometric regions can be sampled by using RandomPoint.

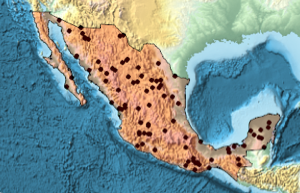
Create a country polygon.

In[1]:=

region = DiscretizeGraphics[CountryData["Mexico", "Polygon"], ImageSize -> Medium]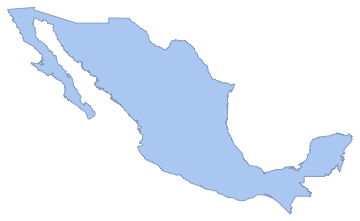

Out[1]=

Define a function that does the sampling of the Poisson point process with three arguments: region, intensity, and number of realizations.

In[2]:=

ppp[region_, intensity_, n_] := Module[{nlist, pts}, nlist = RandomVariate[PoissonDistribution[intensity RegionMeasure[region]], n]; pts = RandomPoint[region, Total[nlist]]; nlist = Accumulate[nlist]; nlist = Transpose[{Prepend[Most[nlist] + 1, 1], nlist}]; Table[Take[pts, ind], {ind, nlist}] ]

Generate a realization of the Poisson point process in the country polygon with intensity 0.5 and visualize it with Graphics.

In[3]:=

intensity = 0.5; sample = ppp[region, intensity, 1];

In[4]:=

Show[region, Graphics[{Black, Point @@ sample}]]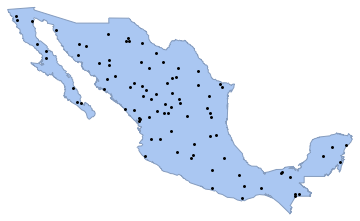

Out[4]=

Generate 10⁴ samples from the same process. The total number of points in each sample satisfies PoissonDistribution, with the mean equal to intensity times the area of the region.

In[5]:=

samples = ppp[region, intensity, 10^4]; counts = Length /@ samples;

In[6]:=

htd = PearsonChiSquareTest[counts, PoissonDistribution[intensity RegionMeasure[region]], "HypothesisTestData"];

In[7]:=

htd["TestDataTable"]

Out[7]=

In[8]:=

htd["TestConclusion"]

Out[8]=

The number of points in any subregion is also Poisson distributed. Here, this is examined with a disk that lies within the polygon, and the number of points in it is counted.

In[9]:=

disk1 = Disk[{-107, 28}, 1.5]; Show[region, Graphics[{Red, disk1}]]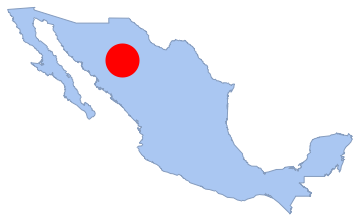

Out[9]=

In[10]:=

memberfun1 = RegionMember[disk1]; counts1 = Table[Total[Boole[memberfun1[pts]]], {pts, samples}];

Perform PearsonChiSquareTest on the number of counts with a Poisson distribution.

In[11]:=

htd = PearsonChiSquareTest[counts1, PoissonDistribution[intensity RegionMeasure[disk1]], "HypothesisTestData"];

In[12]:=

htd["TestDataTable"]

Out[12]=

In[13]:=

htd["TestConclusion"]

Out[13]=

The number of points in any disjoint subregions is independent. Here, the number of points in two disjoint disks is counted, and the SpearmanRankTest is performed.

In[14]:=

disk2 = Disk[{-100, 20}, 1.3]; Show[region, Graphics[{Red, disk1, Blue, disk2}]]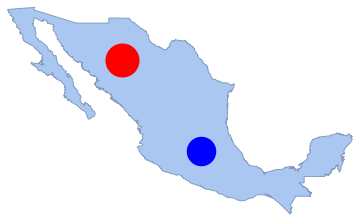

Out[14]=

In[15]:=

memberfun2 = RegionMember[disk2]; counts2 = Table[Total[Boole[memberfun2[pts]]], {pts, samples}];

In[16]:=

htd = SpearmanRankTest[counts1, counts2, "HypothesisTestData"];

In[17]:=

htd["TestDataTable"]

Out[17]=

In[18]:=

htd["TestConclusion"]

Out[18]=