‹›Extended Probability & StatisticsFaster Distribution Estimation
Version 11 adds numerous improvements to distribution estimation, especially in performance. The following charts show the timings for estimating several distributions with different sample sizes. Experiments were performed on a Windows 10 system with an Intel Xeon Processor E3-1245 v2 3.40 GHz. The number at the bottom shows how much faster Version 11 is than Version 10.
Student 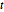 distribution.
distribution.
show complete Wolfram Language input
dist = StudentTDistribution[loc, sc, df];
ndist = StudentTDistribution[-1, 1, 2];
Table[
sample = BlockRandom[SeedRandom["MarketingExample"];
RandomVariate[ndist, n]];
Mean[Table[
First[AbsoluteTiming[EstimatedDistribution[sample, dist];]], {5}]]
, {n, {10, 100, 1000}}]
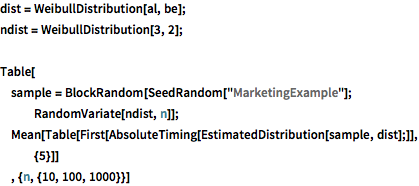
Weibull distribution.
show complete Wolfram Language input
dist = WeibullDistribution[al, be];
ndist = WeibullDistribution[3, 2];
Table[
sample = BlockRandom[SeedRandom["MarketingExample"];
RandomVariate[ndist, n]];
Mean[Table[
First[AbsoluteTiming[EstimatedDistribution[sample, dist];]], {5}]]
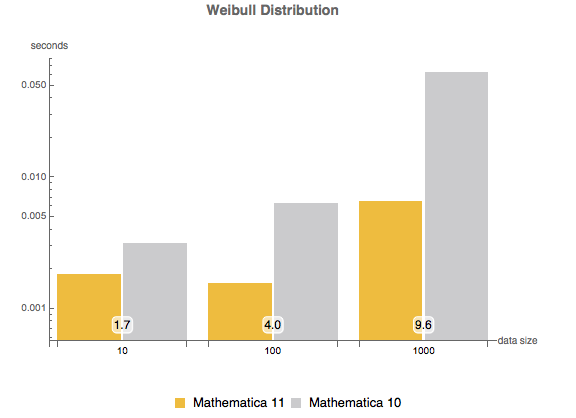
, {n, {10, 100, 1000}}]Mixture of binormal distributions.
show complete Wolfram Language input
dist = MixtureDistribution[{w1,
w2}, {BinormalDistribution[{m11, m12}, {s11, s12}, \[Rho]1],
BinormalDistribution[{m21, m22}, {s21, s22}, \[Rho]2]}];
ndist = MixtureDistribution[{0.3,
0.7}, {BinormalDistribution[{0, 1}, {0.5, 0.25}, 0.7],
BinormalDistribution[{-0.5, 0}, {0.5, 0.25}, 0.1]}];
Table[
sample = BlockRandom[SeedRandom["MarketingExample"];
RandomVariate[ndist, n]];
Mean[Table[
First[AbsoluteTiming[
TimeConstrained[EstimatedDistribution[sample, dist];,
100]]], {5}]]
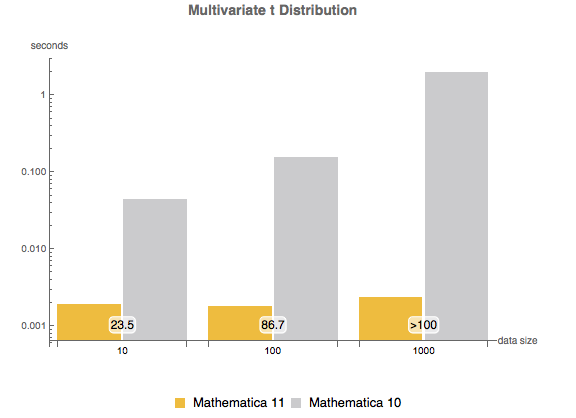
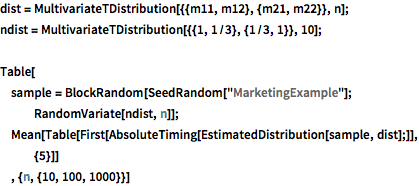
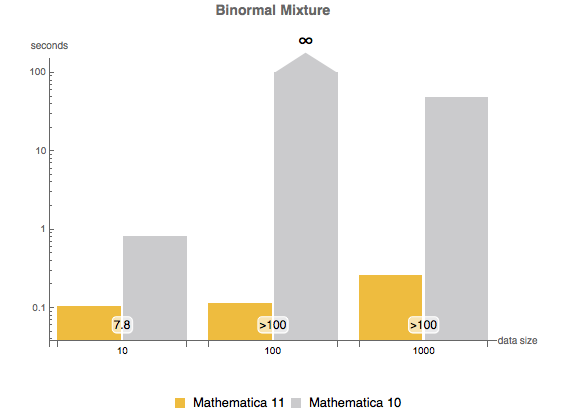
, {n, {10, 100, 1000}}]Multivariate 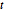 distribution.
distribution.
show complete Wolfram Language input
dist = MultivariateTDistribution[{{m11, m12}, {m21, m22}}, n];
ndist = MultivariateTDistribution[{{1, 1/3}, {1/3, 1}}, 10];
Table[
sample = BlockRandom[SeedRandom["MarketingExample"];
RandomVariate[ndist, n]];
Mean[Table[
First[AbsoluteTiming[EstimatedDistribution[sample, dist];]], {5}]]
, {n, {10, 100, 1000}}]
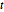 distribution.
distribution.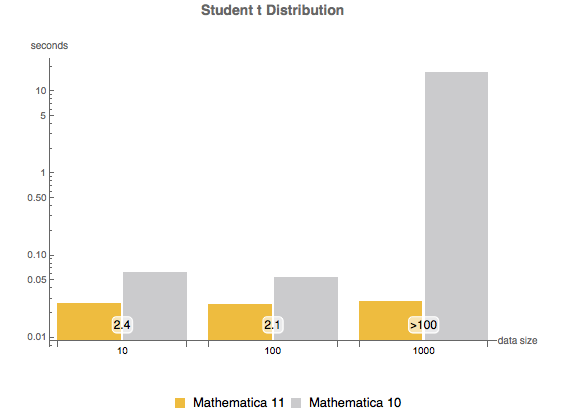
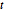 distribution.
distribution.