Handle Discontinuities in a CDF

Define a formula distribution by a cumulative distribution function. The distribution function contains jump discontinuities, which represent a mixture of continuous and discrete components.

In[1]:=

cdf = CDF[ MixtureDistribution[{1/3, 2/3}, {LaplaceDistribution[0, 1], TransformedDistribution[x - 2, x \[Distributed] BinomialDistribution[4, 1/3]]}], z];

In[2]:=

Plot[cdf, {z, -5, 5}, PlotTheme -> "Detailed", Filling -> Axis, ImageSize -> Medium, PlotLegends -> None]

Out[2]=

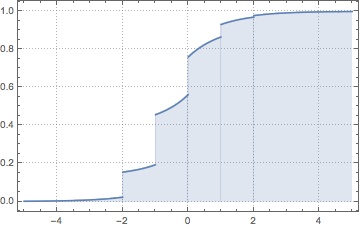
ProbabilityDistribution decomposes the distribution into absolutely continuous and discrete parts.

In[3]:=

ProbabilityDistribution[{CDF, cdf}, {z, -Infinity, Infinity}]

Out[3]=

Handle PDF input with DiracDelta weights.

In[4]:=

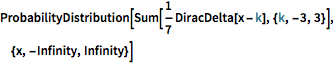
ProbabilityDistribution[ Sum[1/7 DiracDelta[x - k], {k, -3, 3}], {x, -Infinity, Infinity}]

Out[4]=