More Automatic Simplification for Transformed Distributions

Version 11 adds more automatic simplification rules for transformed distributions.

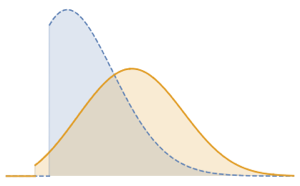
The power of a uniformly distributed random variable is beta distributed.

In[1]:=

TransformedDistribution[X^a, X \[Distributed] UniformDistribution[]]

Out[1]=

The ratio of independent exponentially distributed random variables satisfies the Pareto distribution.

In[2]:=

TransformedDistribution[ X/Y, {X \[Distributed] ExponentialDistribution[b], Y \[Distributed] ExponentialDistribution[a]}]

Out[2]=

The inverse square of a normally distributed random variable is Lévy distributed.

In[3]:=

TransformedDistribution[X^(-2), X \[Distributed] NormalDistribution[0, s]]

Out[3]=

More examples can be found in the following table.

In[4]:=

SetAttributes[fun, HoldFirst]; fun[x_] := {HoldForm[x], x}; Grid[Map[Style[#, ScriptLevel -> 0] &, Join[{{"Transformed Distribution", "Simplified Distribution"}}, { fun[TransformedDistribution[ Min[Subscript[X, 1], Subscript[X, 2]], {Subscript[X, 1] \[Distributed] BernoulliDistribution[Subscript[p, 1]], Subscript[X, 2] \[Distributed] BernoulliDistribution[Subscript[p, 2]]}]], fun[TransformedDistribution[1/X, X \[Distributed] LogLogisticDistribution[\[Gamma], \[Sigma]]]], fun[TransformedDistribution[k*X, X \[Distributed] ChiDistribution[\[Nu]]]], fun[TransformedDistribution[1/X, X \[Distributed] BetaPrimeDistribution[a, b]]], fun[TransformedDistribution[k*Exp[-X], X \[Distributed] ExponentialDistribution[a]]], fun[TransformedDistribution[-Log[X], X \[Distributed] PowerDistribution[1, a]]], fun[TransformedDistribution[c*X, X \[Distributed] ChiSquareDistribution[a]]], fun[TransformedDistribution[1 + X, X \[Distributed] ExponentialDistribution[a]]], fun[TransformedDistribution[ Sqrt[X*Y], {X \[Distributed] ExponentialDistribution[m], Y \[Distributed] GammaDistribution[a, b]}]], fun[TransformedDistribution[Log[X]/2, X \[Distributed] FRatioDistribution[n, m]]], fun[TransformedDistribution[R^2, R \[Distributed] RiceDistribution[\[Nu], 1]]] }], {2}], Dividers -> All, Spacings -> {4, 2}, Background -> {None, {{None, GrayLevel[.9]}}, {{1, 1} -> Hue[.6, .4, 1], {1, 2} -> Hue[.6, .4, 1]}}, BaseStyle -> {FontFamily -> Times, FontSize -> 13}, Alignment -> {Center, Center}] // TraditionalForm

Out[4]//TraditionalForm=