Estimation of Irregularly Sampled Random Processes

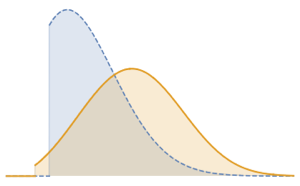
Generate a realization of an irregularly sampled OrnsteinUhlenbeckProcess.

In[1]:=

sample = TimeSeriesResample[ RandomFunction[ OrnsteinUhlenbeckProcess[0, .1, .3], {0, 100, .1}], {Sort[ RandomReal[100, 1000]]}]

Out[1]=

In[2]:=

ListLinePlot[sample, Filling -> Axis, ImageSize -> Medium, PlotTheme -> "Detailed"]

Out[2]=

Estimate the process parameters from irregularly sampled data.

In[3]:=

EstimatedProcess[sample, OrnsteinUhlenbeckProcess[\[Mu], \[Sigma], \[Theta]]]

Out[3]=

Retrieve the stock prices for GE since January 1, 2013, and convert them to TemporalData .

In[4]:=

price = TemporalData[FinancialData["GE", "Jan. 1, 2013"]]

Out[4]=

In[5]:=

DateListPlot[price, Filling -> Axis, ImageSize -> Medium, PlotTheme -> "Detailed"]

Out[5]=

The time stamp of the stock price data is nonuniform.

In[6]:=

MinMax[Differences[price["Times"]]]

Out[6]=

Assume the log price satisfies FractionalBrownianMotionProcess and estimate the parameters.

In[7]:=

EstimatedProcess[Log[price], FractionalBrownianMotionProcess[\[Mu], \[Sigma], h]]

Out[7]=