Sample from a Polynomial Density

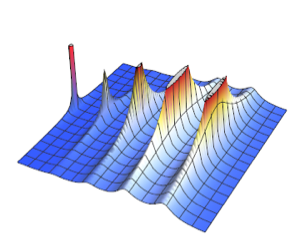
Define a multivariate formula distribution with a polynomial probability density function.

In[1]:=

dist = ProbabilityDistribution[ \[FormalX]1 (1 - \[FormalX]1 (1 - \ \[FormalX]2) \[FormalX]2), {\[FormalX]1, 0, 1}, {\[FormalX]2, 0, 1}, Method -> "Normalize"]

Out[1]=

The density integrates to 1 in the given domain.

In[2]:=

Integrate[PDF[dist, {x, y}], {x, 0, 1}, {y, 0, 1}]

Out[2]=

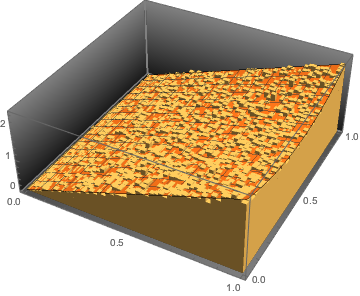
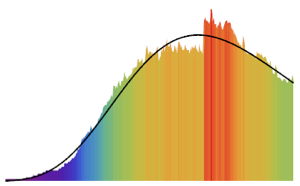
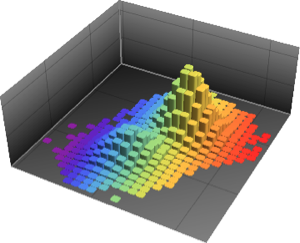
Sample from the distribution and compare the histogram with the density function.

In[3]:=

Show[Histogram3D[RandomVariate[dist, 10^6], 40, "PDF"], Plot3D[PDF[dist, {x, y}] // Evaluate, {x, 0, 1}, {y, 0, 1}, PlotTheme -> "Marketing"], ImageSize -> Medium]

Out[3]=