Sample Points from Regions

RandomPoint samples a pseudorandom point set uniformly in a given region.

In[1]:=

Graphics[{Polygon[CirclePoints[5]], White, Point[RandomPoint[Polygon[CirclePoints[5]], 200]]}, ImageSize -> Medium]

Out[1]=

Sample points in an implicit Lissajous region.

In[2]:=

\[ScriptCapitalR] = ImplicitRegion[-1 + (-1 + 18 x^2 - 48 x^4 + 32 x^6)^2 + (-1 + 18 y^2 - 48 y^4 + 32 y^6)^2 <= 0, {x, y}];

In[3]:=

Graphics[{PointSize[Tiny], Point[RandomPoint[\[ScriptCapitalR], 10^4]]}, ImageSize -> Medium]

Out[3]=

Sample points from a Text primitive.

In[4]:=

mr = DiscretizeGraphics[Text[Style["\[CapitalSigma]", Bold]], _Text, MaxCellMeasure -> 0.1];

In[5]:=

Graphics[{PointSize[Tiny], Point[RandomPoint[mr, 10000]]}, ImageSize -> Medium]

Out[5]=

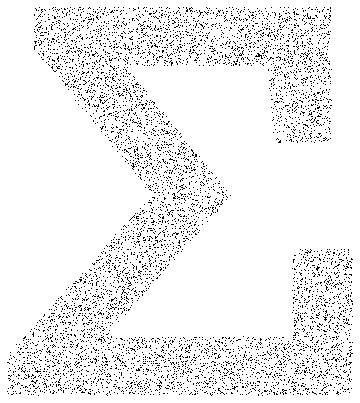
Use the Monte Carlo method to approximate an integral with a domain in a parametric region.

In[6]:=

region = ParametricRegion[{{s, s t}, s^2 + t^2 <= 1}, {s, t}];

In[7]:=

RegionPlot[region, ImageSize -> Medium, PlotTheme -> "Detailed", PlotLegends -> None]

Out[7]=

The function to be integrated over the domain.

In[8]:=

f[{x_, y_}] := x^3 - 2 x^2 y + 4 x^6 - y^5; val = NIntegrate[f[{x, y}], {x, y} \[Element] region]

Out[8]=

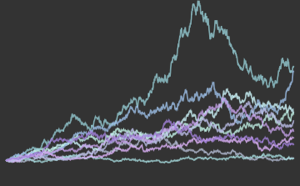
Visualize the convergence of the Monte Carlo statistic as the sample size increases.

In[9]:=

ListLogLogPlot[ Transpose[{2^Range[20], ParallelTable[ RegionMeasure[region] Mean[f /@ RandomPoint[region, 2^n]], {n, 1, 20}]}], PlotRange -> All, PlotTheme -> "Detailed", ImageSize -> Medium, Joined -> True, Filling -> val]

Out[9]=