Improved Performance of Data Binning

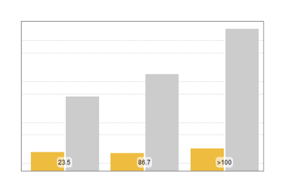
Compare timings for data binning. The following charts show the speed comparisons for different sample sizes and bin specifications. Experiments were performed on a Windows 10 system with an Intel Xeon Processor E3-1245 v2 3.40 GHz. The number at the bottom shows how much faster Version 11 is than Version 10.

One-dimensional nonuniform bins.

In[1]:=

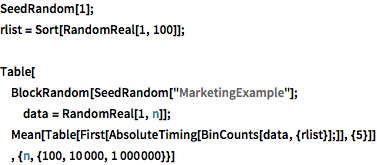
SeedRandom[1]; rlist = Sort[RandomReal[1, 100]]; Table[ BlockRandom[SeedRandom["MarketingExample"]; data = RandomReal[1, n]]; Mean[Table[First[AbsoluteTiming[BinCounts[data, {rlist}];]], {5}]] , {n, {100, 10000, 1000000}}]

Out[139]=

Two-dimensional nonuniform bins.

In[2]:=

SeedRandom[1]; rlist1 = Sort[RandomReal[1, 100]]; rlist2 = Sort[RandomReal[1, 100]]; Table[ BlockRandom[SeedRandom["MarketingExample"]; data = RandomReal[1, {n, 2}]]; Mean[Table[ First[AbsoluteTiming[BinCounts[data, {rlist1}, {rlist2}];]], {5}]] , {n, {100, 10000, 1000000}}]

Out[141]=

One-dimensional uniform bins.

In[3]:=

Table[ BlockRandom[SeedRandom["MarketingExample"]; data = RandomReal[1, n]]; Mean[Table[First[AbsoluteTiming[BinCounts[data, {0, 1, 0.1}];]], {5}]] , {n, {10000, 100000, 1000000}}]

Out[143]=

Two-dimensional uniform bins.

In[4]:=

Table[ BlockRandom[SeedRandom["MarketingExample"]; data = RandomReal[1, {n, 2}]]; Mean[Table[ First[AbsoluteTiming[ BinCounts[data, {0, 1, 0.1}, {0, 1, 0.1}];]], {5}]] , {n, {10000, 100000, 1000000}}]

Out[145]=