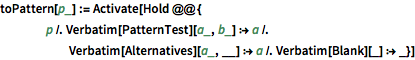特殊関数の導関数ネットワーク

Wolfram言語は300以上の組込みの数学関数を含んでいる．これらの関数のそれぞれに微分操作を適用することを考えてみよう．多くの場合，微分の結果として1つあるいは複数の新たな関数が現れる． これらの連結を数量化すると，シンボルとその操作の関係の興味深い研究ができる．特に，次の例は低次の微分から発生したネットワークを導き出すものである．

初等微積分で学んだように，自然対数の微分は逆関数を与える．

In[1]:=

D[Log[x], x]

Out[1]=

一方，ある種の関数については，もとの関数から導関数が直接表現できる．

In[2]:=

D[ProductLog[x], x]

Out[2]=

MathematicalFunctionDataの"LowOrderDerivatives" 特性は，すべての導関数に素早く簡単にアクセスできるようにする．

In[3]:=

Entity["MathematicalFunction", "EllipticF"][ EntityProperty["MathematicalFunction", "LowOrderDerivatives"]] // TraditionalForm

Out[3]//TraditionalForm=

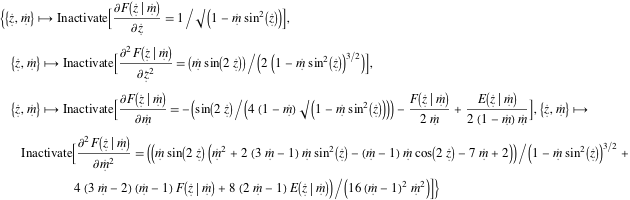
微分後の関数を識別するために，すべての関数とその引数パターンを集める（よく現れるベキを避けるために，ベキ関数と平方根関数は無視する）．例えば，恒等式に基づいて，関数Secは関数Tanとそれ自身を含み，結果として2つの連結が作成されることになる．

In[4]:=

allFunctions = DeleteCases[MathematicalFunctionData[], Entity["MathematicalFunction", "Sqrt"] | Entity["MathematicalFunction", "Power"]];

In[5]:=

patts = EntityValue[allFunctions, EntityProperty["MathematicalFunction", "ArgumentPattern"]];

In[6]:=

toPattern[p_] := Activate[Hold @@ { p /. Verbatim[PatternTest][a_, b_] :> a /. Verbatim[Alternatives][a_, __] :> a /. Verbatim[Blank][_] :> _}]

In[7]:=

pairs = {#1, toPattern[#2]} & @@@ Transpose[{allFunctions, patts}];

In[8]:=

(identify[#2] = #1) & @@@ pairs;

In[9]:=

makeConnection[f1_, id_] := Module[{indices, heldSubexpressions, f2List, \[ScriptCapitalF]\[GothicCapitalF]}, indices = Quiet[Cases[ MapIndexed[\[ScriptCapitalF]\[GothicCapitalF], id, {0, \[Infinity]}], _\[ScriptCapitalF]\[GothicCapitalF], \ \[Infinity]][[All, -1]]]; heldSubexpressions = Union[Extract[id, indices, Hold]]; f2List = Union[Last /@ DeleteCases[({#1, identify[#1]} & /@ heldSubexpressions), {_, _identify}]]; {f1 \[DirectedEdge] #, id /. HoldPattern[Function[_, Inactivate[x_]]] :> HoldForm[x]} & /@ f2List]

In[10]:=

makeConnection[Entity["MathematicalFunction", "Sec"] , Function[{x}, Inactivate[D[Sec[x], x] == Sec[x] Tan[x]]]]

Out[10]=

すべての導関数を分析し，自明な自己ループはすべて結果のグラフから除外して，結果のグラフ構造を可視化する．

In[11]:=

\[Lambda]F = Length[allFunctions]; Monitor[ allConnections = Table[ fD = allFunctions[[\[ScriptJ]]]; derivatives = Activate[ allFunctions[[\[ScriptJ]]][ EntityProperty["MathematicalFunction", "LowOrderDerivatives"]] /. HoldPattern[Power[E, z_]] :> Exp[z]]; connections = If[derivatives === Missing["NotAvailable"], {}, {#[[1, 1]], SortBy[#[[All, -1]], LeafCount]} & /@ GatherBy[ Flatten[makeConnection[fD, #] & /@ derivatives, 1] // Union, First]], {\[ScriptJ], \[Lambda]F}];, Row[{"function ", \[ScriptJ], " of ", \[Lambda]F, ": ", fD}]];

In[12]:=

gr = Graph[Flatten[allConnections, 1][[All, 1]]]

Out[12]=

連結数を数える．

In[13]:=

Flatten[allConnections, 1] // Length

Out[13]=

自己ループを求める．

In[14]:=

selfLoops = Select[ConnectedComponents[ Graph[Flatten[allConnections /. DirectedEdge -> UndirectedEdge, 1][[All, 1]]]], Length[#] == 1 &]

Out[14]=

微分の下で閉じている関数群を求め，ラベル付きのグラフとして可視化する．

In[15]:=

smallLoops = Select[ConnectedComponents[ Graph[Flatten[allConnections /. DirectedEdge -> UndirectedEdge, 1][[All, 1]]]], 1 < Length[#] < 20 &];

In[16]:=

Graph[Select[Flatten[allConnections, 1], MemberQ[#, Alternatives @@ Flatten[smallLoops], \[Infinity]] &][[ All, 1]], VertexLabels -> ((# -> MapAt[Nothing &, CommonName[#], {{1, 1}}]) & /@ Union[Flatten[smallLoops]])]

Out[16]=

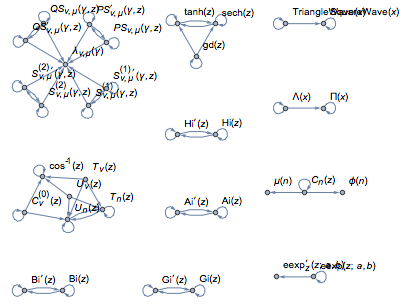
ほとんどの関数がグラフの巨大成分の一部である．頂点上にマウスを動かすと関数が，辺の上に動かすと関数を連結する導関数が見られる．

In[17]:=

allConnectionsRest = Select[Flatten[allConnections, 1], FreeQ[#, Alternatives @@ Flatten[{selfLoops, smallLoops}], \[Infinity]] &];

In[18]:=

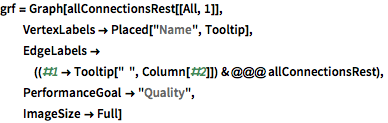
grf = Graph[allConnectionsRest[[All, 1]], VertexLabels -> Placed["Name", Tooltip], EdgeLabels -> ((#1 -> Tooltip[" ", Column[#2]]) & @@@ allConnectionsRest), PerformanceGoal -> "Quality", ImageSize -> Full]

Out[18]=

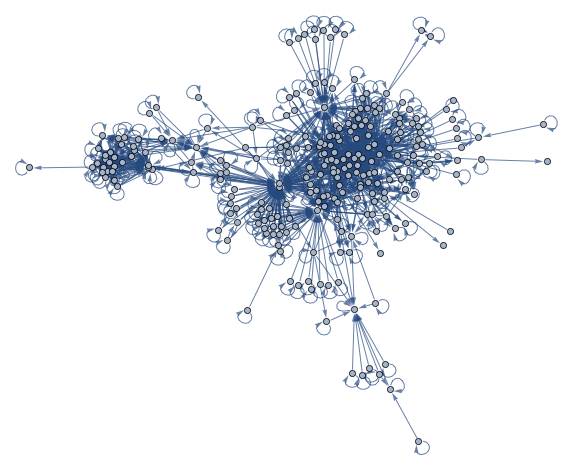
グラフをコミュニティに分割して楕円関数，超幾何関数，窓関数，ゼータ関数，その他幾つかの関数を示す．

In[19]:=

CommunityGraphPlot[grf, FindGraphCommunities[grf, Method -> "Modularity"]]

Out[19]=