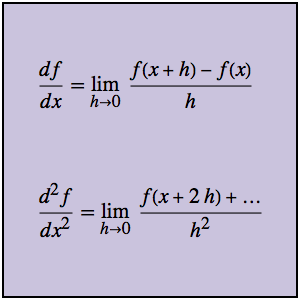Berechnen Sie Differenzenquotienten
Die Wolfram Language kann nicht nur den wohlbekannten univariaten Differenzenquotienten, sondern auch multivariate Quotienten und Quotienten höherer Ordnung berechnen.
In die Zwischenablage kopieren.
In[1]:=
✖
DifferenceQuotient[f[x], {x, h}]Out[1]=
Der Differenzenquotient zweiter Ordnung ist der Differenzenquotient des Quotienten erster Ordnung.
In die Zwischenablage kopieren.
In[2]:=
✖
DifferenceQuotient[f[x], {x, 2, h}]Out[2]=
In die Zwischenablage kopieren.
In[3]:=
✖
DifferenceQuotient[f[x], {x, h}];
DifferenceQuotient[f[x], {x, 2, h}];
% == DifferenceQuotient[%%, {x, h}]Out[3]=
Berechnen Sie einen multivariaten Differenzenquotienten.
In die Zwischenablage kopieren.
In[4]:=
✖
DifferenceQuotient[(x + y + 1)/(((x^2 + 3) (y + 5))), {x, h}, {y, k}]Out[4]=

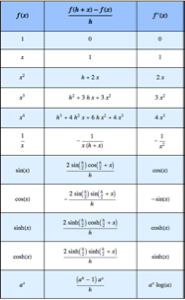
Erstellen Sie eine Tabelle mit wachsenden Differenzenquotienten eines Polynoms, resultierend in Polynomen abnehmender Ordnung.
In die Zwischenablage kopieren.
In[5]:=
✖
Grid[Table[
DifferenceQuotient[x^3 y^2 + 5 x y + 11, {x, i, r}, {y, j, s}], {i,
4}, {j, 3}], Spacings -> {2, 1}]Out[5]=