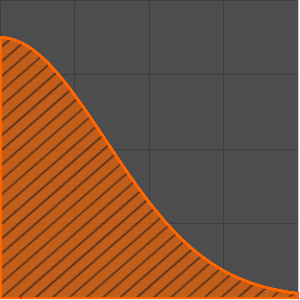
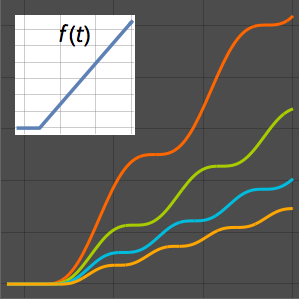
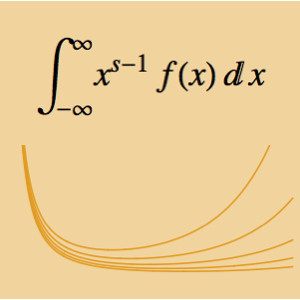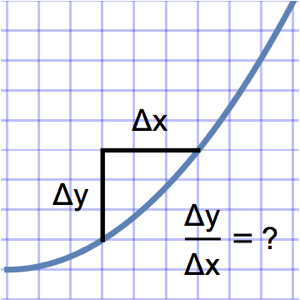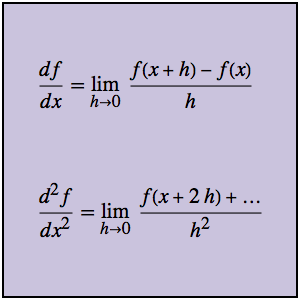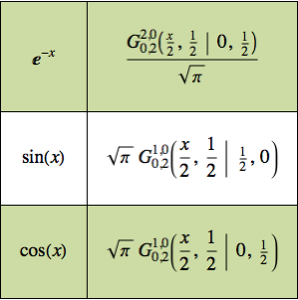Berechnen Sie das Problem der Linie des schnellsten Falles
Beim Problem der Linie des schnellsten Falles geht es darum, die Kurve zu finden, bei der man von jedem Punkt aus die gleiche Zeit benötigt, um zum Tiefpunkt zu gelangen. Wenn Sie die Gesamtfallzeit durch die Bogenlänge der Kurve und die Geschwindigkeit v ausdrücken, ergibt sich die Abelsche Integralgleichung 
. Aus der Definition der unbekannten Funktion 
durch die Beziehung 
und der Verwendung des Energieerhaltungssatzes 
ergibt sich die folgende explizite Gleichung:
abeleqn = T == 1/Sqrt[2 g] \!\(
\*SubsuperscriptBox[\(\[Integral]\), \(0\), \(y\)]\(
\*FractionBox[\(h[z]\),
SqrtBox[\(y - z\)]] \[DifferentialD]z\)\);Lösen Sie mit DSolveValue die Integralgleichung.
dsdy = DSolveValue[abeleqn, h[y], y]
Nutzen Sie den Zusammenhang 
, um nach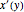 
zu lösen.
dxdy = Sqrt[dsdy^2 - 1]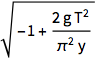
Wenn Sie den Ursprung als Anfangspunkt der Kurve wählen und anschließend integrieren, kann 
als eine Funktion von 
ausgedrückt werden. Nehmen Sie für den Integranden reelle Werte an.
x[y_] = Integrate[dxdy, {y, 0, y},
Assumptions -> (2 g (T^2) )/(\[Pi]^2 y) > 1 && y > 0]
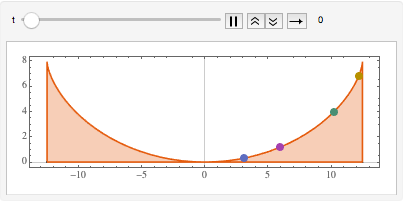
Nehmen Sie eine Fallzeit von zwei Sekunden, bestimmen Sie einen Wert der Schwerebeschleunigung und plotten Sie die maximale Bahn der Tautochrone. (Der Zweig 
kommt von der Lösung 
für die Ableitung von 
.)
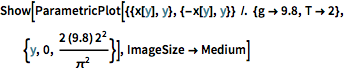
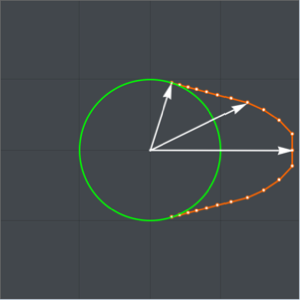
Show[ParametricPlot[{{x[y], y}, {-x[y], y}} /. {g -> 9.8, T -> 2}, {y,
0, (2 (9.8) 2^2)/\[Pi]^2}], ImageSize -> Medium]
Die Variablenänderung 
ergibt eine einfache, nichtsinguläre Parametrisierung der Kurve mit 
.
c[\[Theta]_] = (
g T^2)/\[Pi]^2 {Sin[\[Theta]] + \[Theta], 1 - Cos[\[Theta]]} ;Durch die Kombination des Energieerhaltungssatzes und der Kettenregel 
entsteht die nachstehende Differentialgleichung für 
als eine Funktion von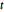 
, die numerisch gelöst werden kann.
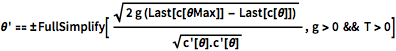
\[Theta]' == \[PlusMinus]FullSimplify[ Sqrt[
2 g (Last[c[\[Theta]Max]] - Last[c[\[Theta]]])] /Sqrt[
c'[\[Theta]].c'[\[Theta]]] , g > 0 && T > 0]
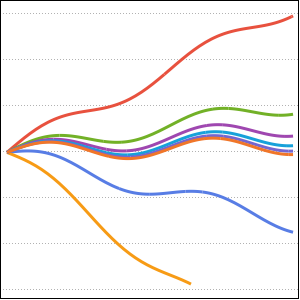
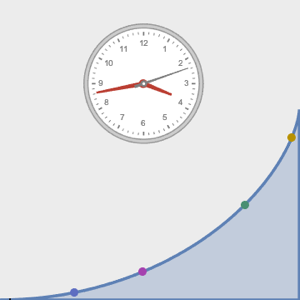
Visualisieren Sie die Bewegung entlang der Tautochrone.
