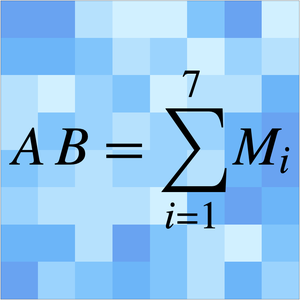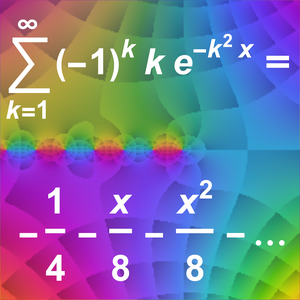Approximate an Exponential Integral (AsymptoticIntegrate)

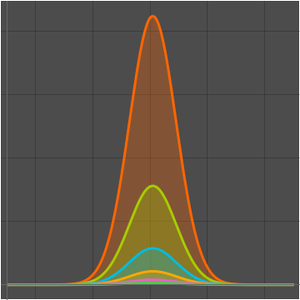
In this example, the asymptotic expansion for an exponential integral depending on a parameter is obtained using Laplace's method. The method relies on an analysis of the integrand in a neighborhood of its maximum.

Define a function involving an exponential kernel that has a maximum at .

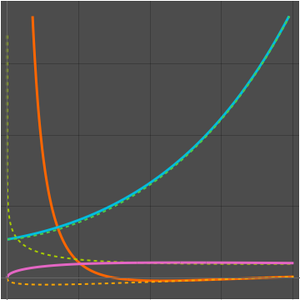
Find the leading term in the expansion of the integral.

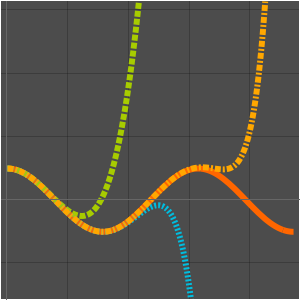
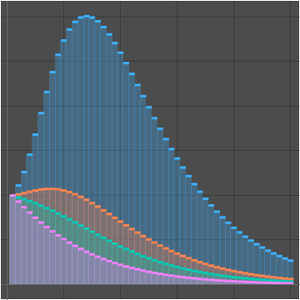
Compare with a numerical approximation.

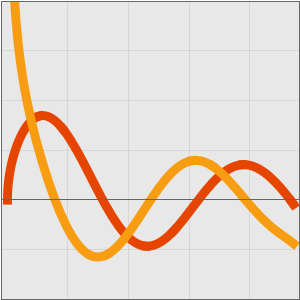
Obtain a better approximation by computing an extra term in the expansion.