Find a Frobenius Approximation (AsymptoticDSolveValue)

A linear ordinary differential equation can be approximated by a Frobenius series 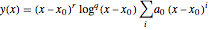near a regular singular point 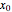for the equation. This example shows how to obtain such an approximation using AsymptoticDSolveValue.

Solve Bessel's equation of order 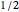around the regular singular point .

In[1]:=1

✖

Out[1]=1

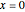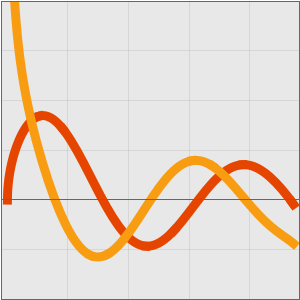
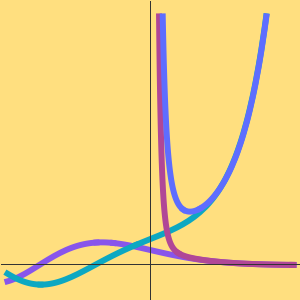
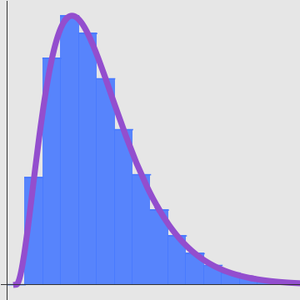
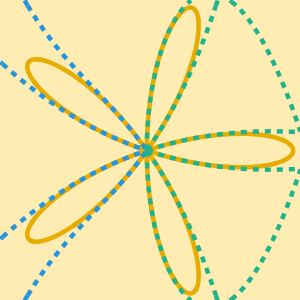
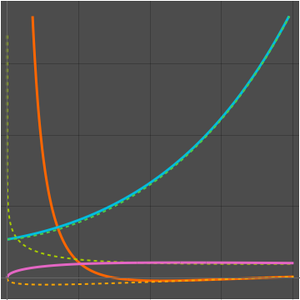
Plot the two components of the general solution. One branch of the solution in this case exhibits a singular behavior near the origin.

In[2]:=2

✖

Out[2]=2

The Frobenius solution may include logarithmic terms, as illustrated in the following.

In[3]:=3

✖

Out[3]=3

The asymptotic approximation happens to be an exact solution in this case.

In[4]:=4

✖

Out[4]=4