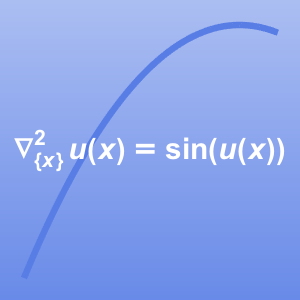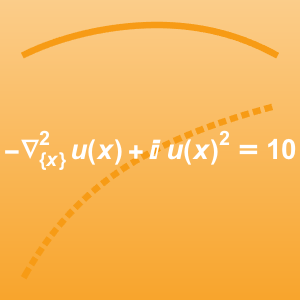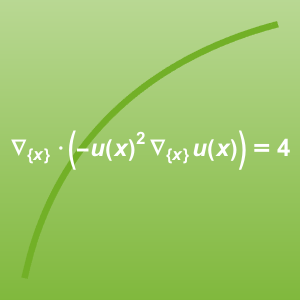Energy Transport
Solve a multi-physics problem that couples the Navier–Stokes equation with a heat equation:

Here  is the vector-valued velocity field,
is the vector-valued velocity field,  is the pressure and
is the pressure and  the identity matrix.
the identity matrix. 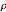 and
and  are the density and dynamic viscosity, respectively.
are the density and dynamic viscosity, respectively.  is the heat capacity of the liquid and
is the heat capacity of the liquid and  the temperature.
the temperature.
Specify parameters and a rectangular region with cutouts.
Visualize the region.
Specify a Prandtl number  and a Rayleigh number
and a Rayleigh number  .
.
Set up a viscous Navier–Stokes equation that is coupled to a heat equation making use of a Boussinesq approximation. Use the material parameters specified.
Set up no-slip boundary conditions for the velocities on all boundary walls.
Set up a reference pressure point.
Specify a temperature difference between the left and right walls.
Replace parameters in the boundary conditions.
Set up initial conditions such that the system is at rest.
Monitor the time-integration progress and the total time it takes to solve the PDE while using a specified mesh spacing and interpolating the velocities  and
and  and the temperature
and the temperature  with second order and the pressure
with second order and the pressure  with first order.
with first order.
Construct a visualization of the boundary of the region.
Visualize the pressure distribution.
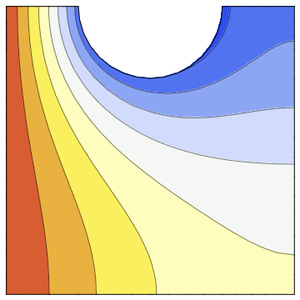
Visualize the temperature distribution.
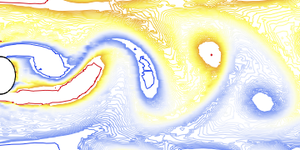
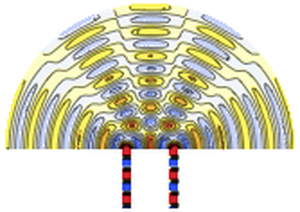
Visualize the velocity field.
Animate the change in temperature and the velocity streamlines.
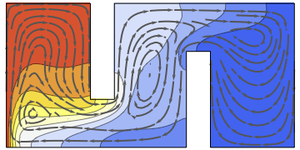
For the curious, investigate the different velocity field produced by simply swapping the cutout positions.