WolframSystèmes de contrôleUn élément essentiel de
Wolfram Language

Modélisez, concevez, déployez.

Modélisez l'environnement. Concevez un contrôleur. Déployez dans le monde réel. Le tout dans un flux de travail hautement intégré, développé pour les étudiants et les professionnels.

Démarrer

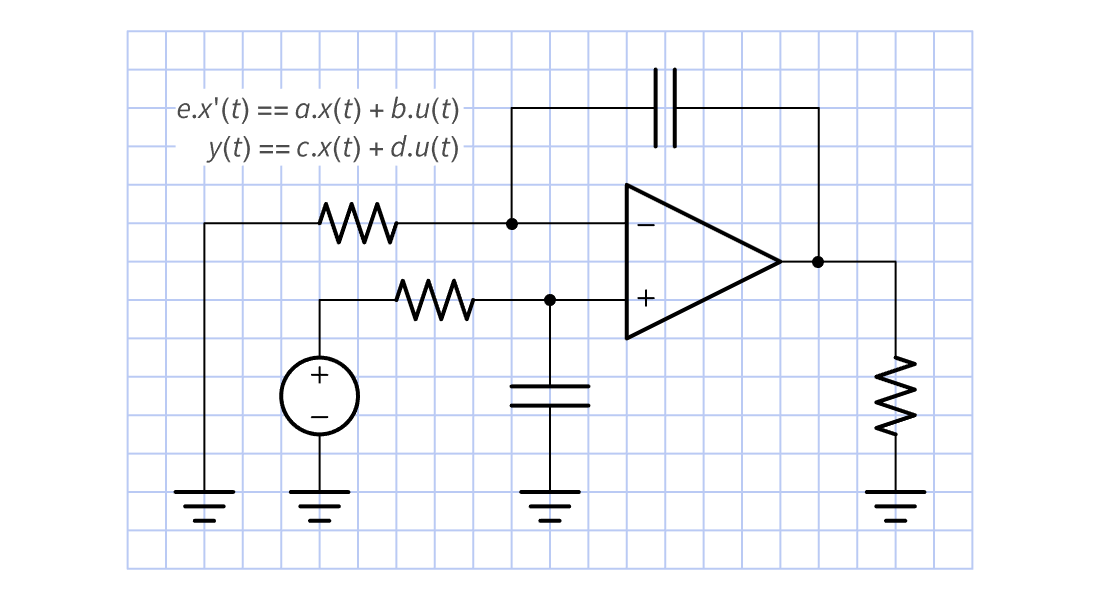
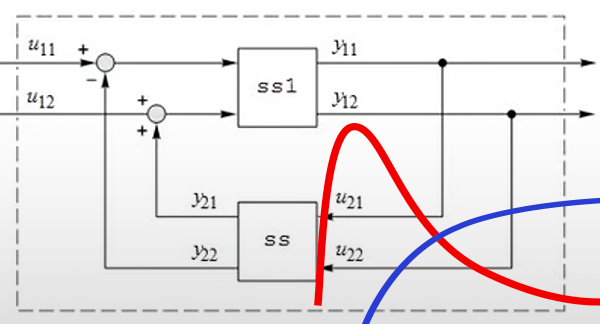
Modèles basés sur des blocs

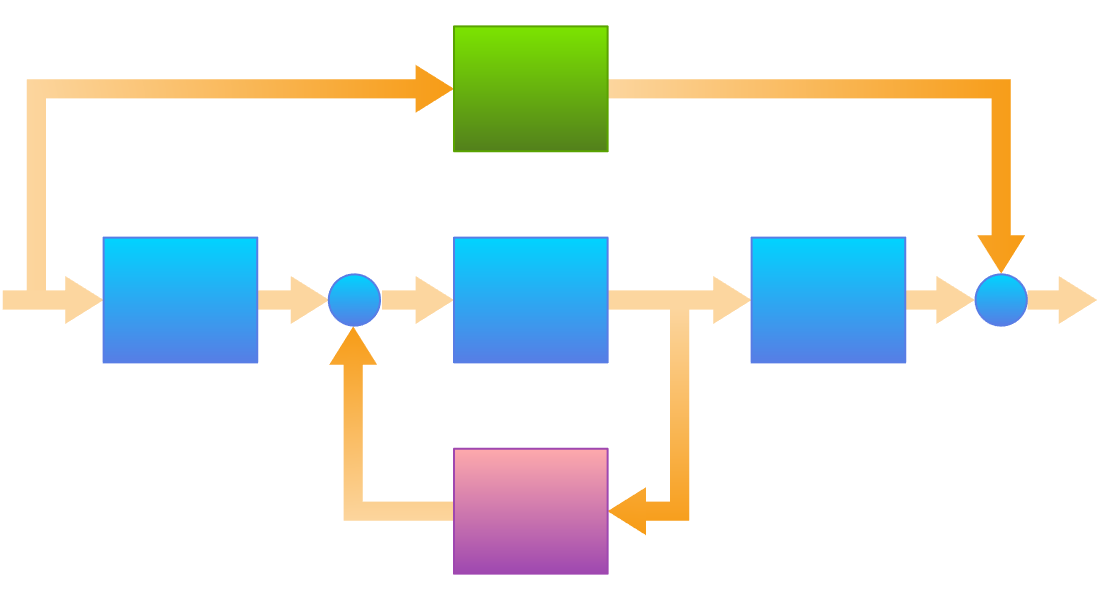
Créez des blocs de modèles d'espace d'état ou de fonction de transfert directement ou à partir d'équations différentielles. Connectez-les pour former des systèmes plus vastes. Utilisez les modèles obtenus pour l'analyse, la conception et le déploiement.

Modèles basés sur des composants

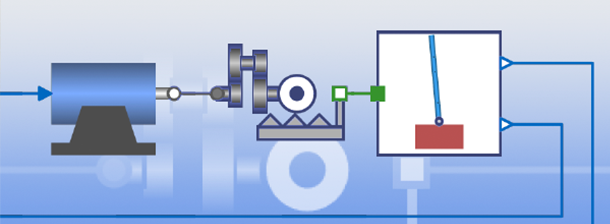
Faites glisser, déposez et connectez les composants du modèle comme des pièces de Lego pour obtenir des modèles multidomaines de haute fidélité. Utilisez-les pour la simulation, la validation et pour dériver des modèles basés sur des blocs pour la conception de commandes.

Conception graphique

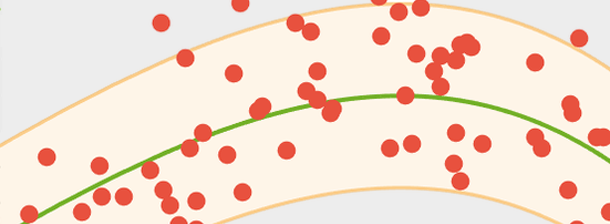
Concevez et analysez des systèmes de contrôle à l'aide de techniques graphiques telles que les diagrammes de Bode, de Nyquist, du locus racine et d'autres diagrammes. Les exemples typiques incluent la conception lead-lag, l'analyse de stabilité et l'analyse de robustesse.

Guide pour l'analyse et la conception graphiques

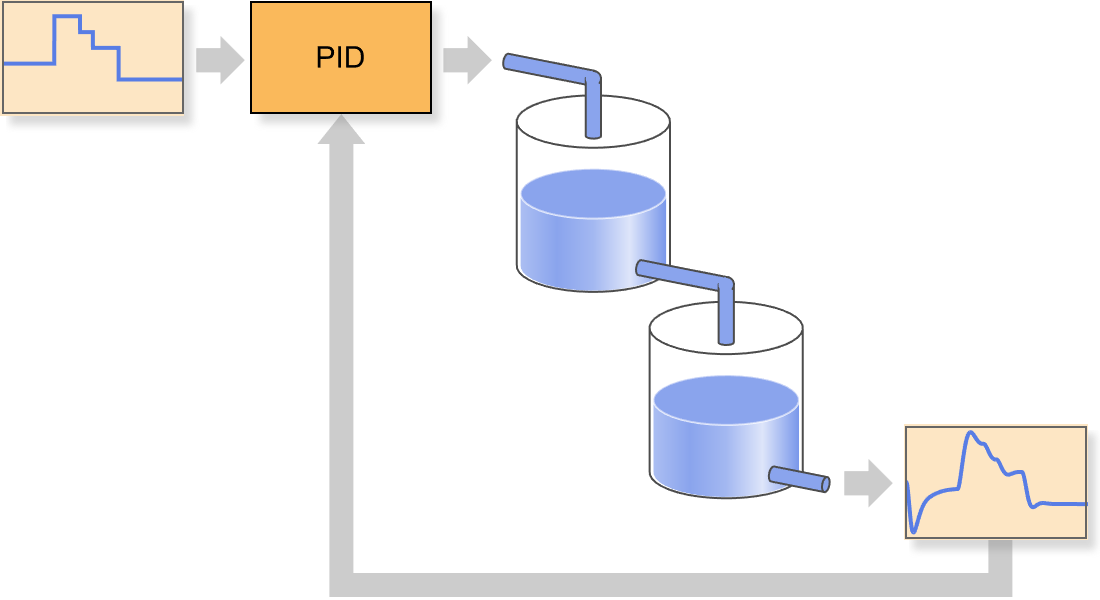
Conception de PID

Réglez automatiquement un régulateur PID sur la base de modèles et de critères de réglage. Améliorez le suivi du système et le rejet des perturbations. Livré avec des stratégies de réglage intégrées, notamment Ziegler–Nichols, Cohen–Coon et bien d'autres encore.

La fonction PIDTune

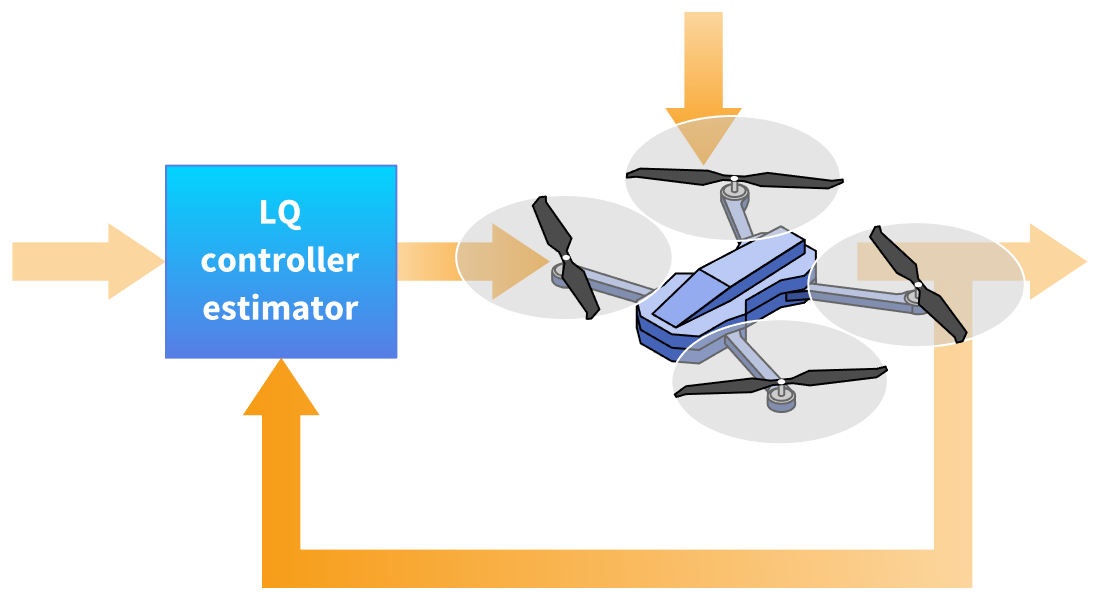
Conception de LQ

Concevez des contrôleurs et des estimateurs à l'aide d'une commande linéaire quadratique (LQ). Résolvez les problèmes de régulation ou de suivi. L'application comprend une prise en charge intégrée des techniques standard, y compris LQR, LQG et Kalman.

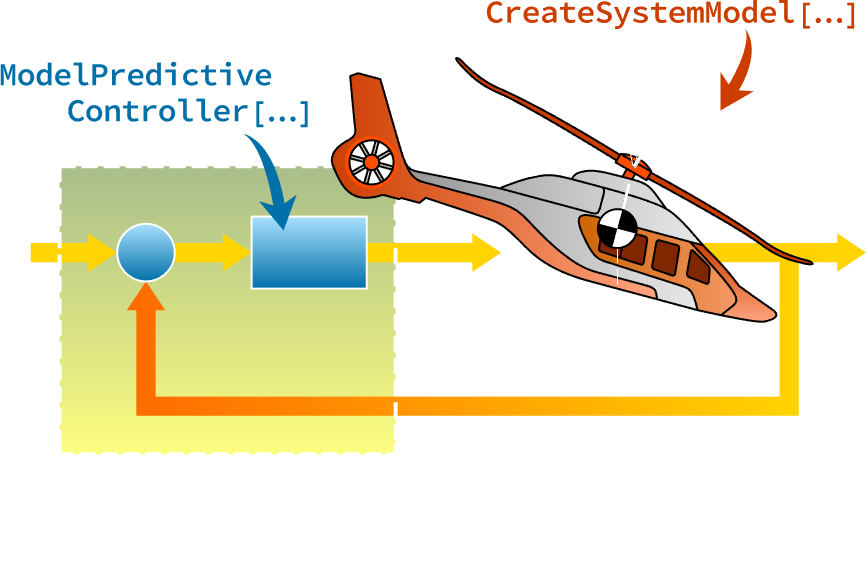
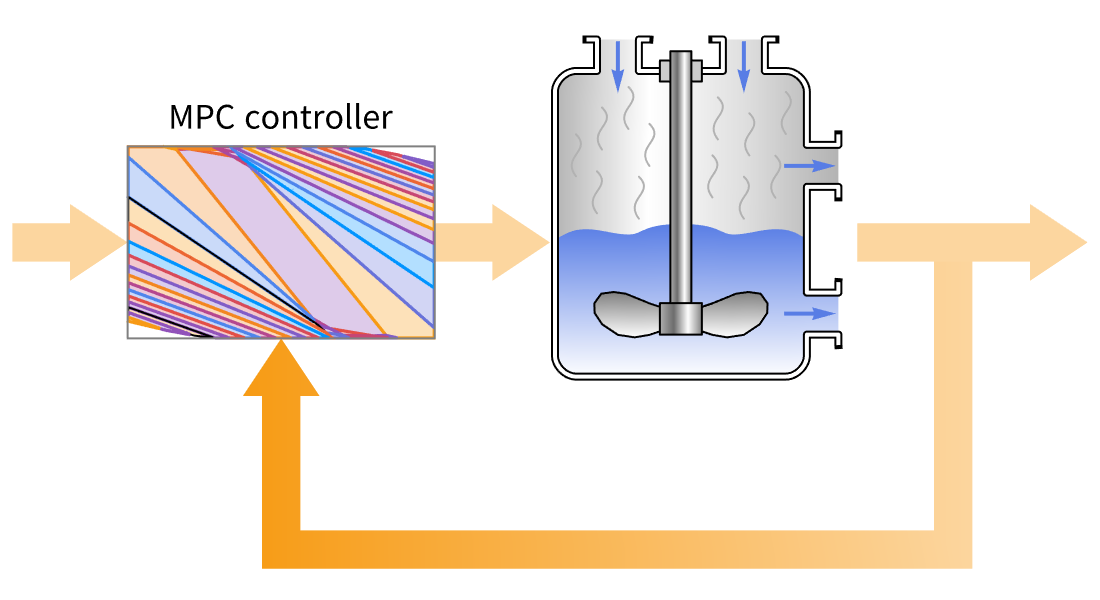
Guide pour la conception à l'aide de modèles espace-état

Conception de MPC

Concevez une commande prédictive de modèle explicites (MPC en anglais) pour les applications à échantillonnage rapide et celles dont la puissance de calcul est limitée, en utilisant automatiquement l'optimisation paramétrique hors ligne. Résolvez les problèmes de régulation linéaire ou de suivi sous contraintes pour la minimisation des coûts normalisés à 1, 2 au carré ou à ∞.

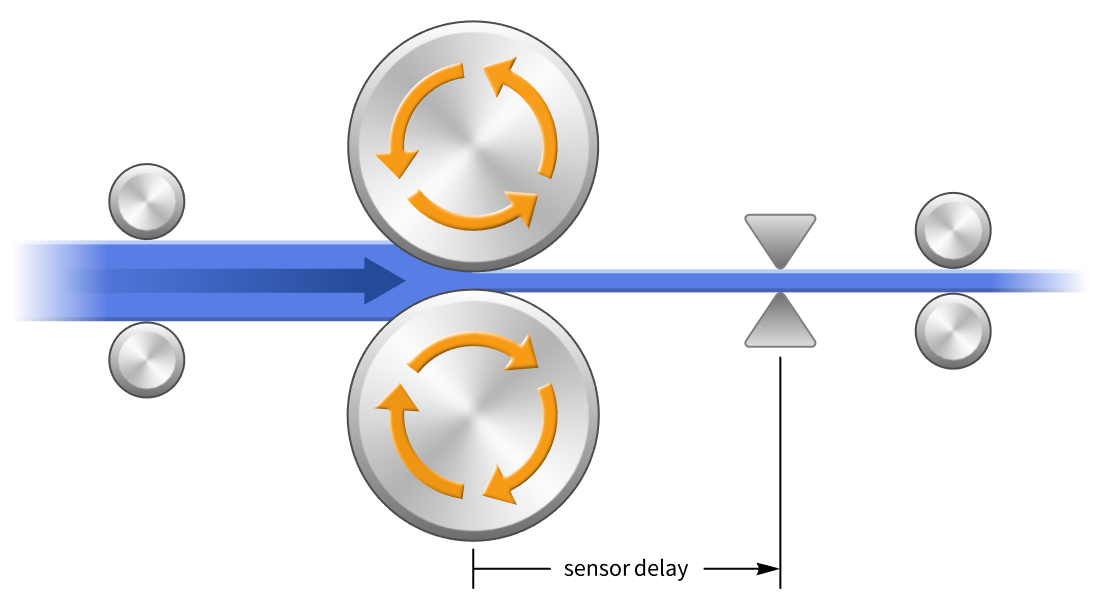
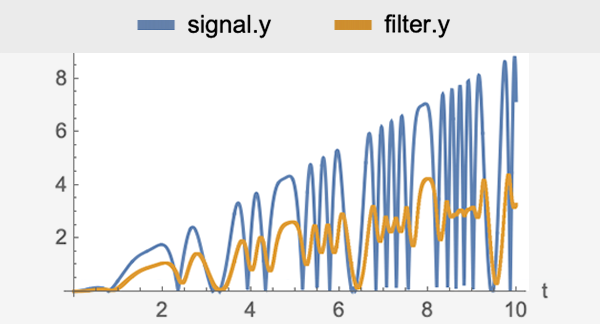
La fonction ModelPredictiveController

Délai et conception des descripteurs

Concevez des contrôleurs pour des modèles avec des retards et un mélange d'équations dynamiques et algébriques. Les retards, dus à des décalages de communication, etc., peuvent provoquer des instabilités s'ils ne sont pas compensés. Utilisez des procédures spéciales telles qu'une commande prédictive de Smith ou réduisez les modèles standard à l'aide d'approximations.

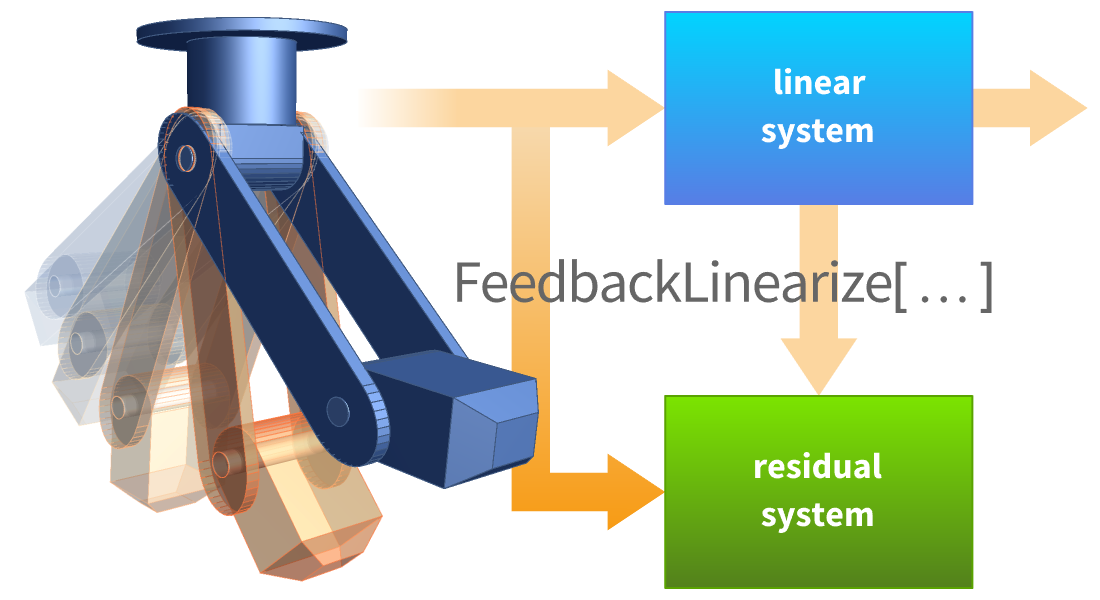
Conception affine et non linéaire

Concevez des contrôleurs non linéaires pour les systèmes dans lesquels les non-linéarités jouent un rôle important. Cela permet de réduire la dégradation des performances dans les régions éloignées du point de fonctionnement. Utilisez des techniques symboliques telles que la linéarisation par rétroaction, la régulation de la sortie, etc.

Déploiement de FMI

Déployez des contrôleurs en tant qu'unités de maquette fonctionnelle (FMU en anglais) dans plus de 100 autres outils compatibles FMI. Collaborez efficacement dans un environnement où les sous-systèmes sont conçus par des entreprises et des outils différents. Identifiez les défauts à un stade précoce et évitez les problèmes majeurs d'intégration en aval.

Déploiement de microcontrôleurs

Générez et déployez automatiquement les conceptions de contrôle et le code d'acquisition de données sur les microcontrôleurs. Éliminez les itérations fastidieuses et sujettes aux erreurs du code source de niveau inférieur.

Live Playground

This is an interactive notebook—try making your own changes!

Continue exploring more examples:Things to Try

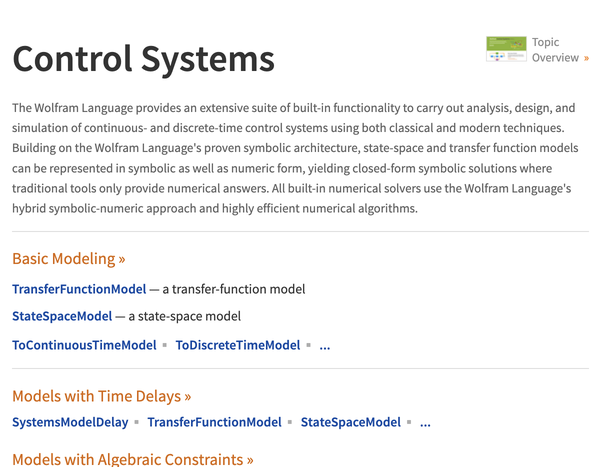
Documentation de Wolfram Systèmes de contrôle

Wolfram Systèmes de contrôle fait partie intégrante de Wolfram Language. Le système complet contient plus de 6000 fonctions intégrées couvrant tous les domaines du calcul, toutes soigneusement intégrées pour fonctionner parfaitement ensemble.

Wolfram Language
Champ d'application et documentation

Guide

Guide pour les systèmes de contrôle

Guide

Guide pour les kits de microcontrôleurs

Guide

Guide pour l'analyse et la conception de modèles de systèmes

AffineStateSpaceModel ▪ AsymptoticOutputTracker ▪ BodePlot ▪ CarlemanLinearize ▪ ContinuousTimeModelQ ▪ ControllabilityGramian ▪ ControllabilityMatrix ▪ ControllableDecomposition ▪ ControllableModelQ ▪ DescriptorStateSpace ▪ DiscreteInputOutputModel ▪ DiscreteLQEstimatorGains ▪ DiscreteLQRegulatorGains ▪ DiscreteTimeModelQ ▪ DualSystemsModel ▪ EstimatorGains ▪ EstimatorRegulator ▪ FeedbackLinearize ▪ FeedbackSector ▪ FeedbackSectorStyle ▪ FeedbackType ▪ FullInformationOutputRegulator ▪ GainMargins ▪ GainPhaseMargins ▪ InternallyBalancedDecomposition ▪ JordanModelDecomposition ▪ KalmanEstimator ▪ KroneckerModelDecomposition ▪ LinearizingTransformationData ▪ LQEstimatorGains ▪ LQGRegulator ▪ LQOutputRegulatorGains ▪ LQRegulatorGains ▪ MinimalStateSpaceModel ▪ ModelPredictiveController ▪ NicholsGridLines ▪ NicholsPlot ▪ NonlinearStateSpaceModel ▪ NyquistGridLines ▪ NyquistPlot ▪ ObservabilityGramian ▪ ObservabilityMatrix ▪ ObservableDecomposition ▪ ObservableModelQ ▪ OutputControllabilityMatrix ▪ OutputControllableModelQ ▪ OutputResponse ▪ PhaseMargins ▪ PhaseRange ▪ PIDData ▪ PIDDerivativeFilter ▪ PIDFeedforward ▪ PIDTune ▪ PoleZeroMarkers ▪ RootLocusPlot ▪ SamplingPeriod ▪ SingularValuePlot ▪ SmithDelayCompensator ▪ StabilityMargins ▪ StabilityMarginsStyle ▪ StateFeedbackGains ▪ StateOutputEstimator ▪ StateResponse ▪ StateSpaceModel ▪ StateSpaceRealization ▪ StateSpaceTransform ▪ StateTransformationLinearize ▪ SystemsConnectionsModel ▪ SystemsModelControllerData ▪ SystemsModelDelay ▪ SystemsModelDelayApproximate ▪ SystemsModelDelete ▪ SystemsModelDimensions ▪ SystemsModelExtract ▪ SystemsModelFeedbackConnect ▪ SystemsModelLabels ▪ SystemsModelLinearity ▪ SystemsModelMerge ▪ SystemsModelOrder ▪ SystemsModelParallelConnect ▪ SystemsModelSeriesConnect ▪ SystemsModelStateFeedbackConnect ▪ SystemsModelVectorRelativeOrders ▪ ToContinuousTimeModel ▪ ToDiscreteTimeModel ▪ TransferFunctionCancel ▪ TransferFunctionExpand ▪ TransferFunctionFactor ▪ TransferFunctionModel ▪ TransferFunctionPoles ▪ TransferFunctionZeros ▪ Eigenvalues ▪ Unevaluated ▪ ZTransform ▪ MatrixExp ▪ LaplaceTransform ▪ MatrixLog ▪ MaxIterations ▪ ZeroTest ▪ PadeApproximant ▪ StandardForm ▪ DiscreteShift ▪ IdentityMatrix ▪ D ▪ Inverse ▪ MAProcess ▪ ARProcess ▪ ARMAProcess ▪ ARIMAProcess ▪ SARIMAProcess ▪ SARMAProcess ▪ CreateSystemModel ▪ SquareWave ▪ Cos ▪ Function ▪ Tolerance ▪ Interval ▪ ListPlot ▪ NRoots ▪ PlotMarkers ▪ UnitStep ▪ NDSolve ▪ RecurrenceTable ▪ DSolve ▪ RSolve ▪ InverseLaplaceTransform ▪ InverseZTransform ▪ GreenFunction ▪ Graphics ▪ LineLegend ▪ Dashed ▪ Dotted ▪ Minimize ▪ JordanDecomposition ▪ Eigensystem ▪ SingularValueDecomposition ▪ Solve ▪ NSolve ▪ Listable ▪ LinearSolve ▪ Sin ▪ MatrixRank ▪ Min ▪ Sort ▪ Max ▪ TemporalData ▪ MissingDataMethod ▪ ResamplingMethod ▪ InterpolationOrder ▪ FoldList ▪ Association ▪ Dataset ▪ RecurrenceFilter ▪ TimeSeries ▪ ListConvolve ▪ Det ▪ MonomialList ▪ Block ▪ AlignmentPoint ▪ Center ▪ AspectRatio ▪ GoldenRatio ▪ Axes ▪ AxesLabel ▪ AxesOrigin ▪ AxesStyle ▪ Background ▪ BaselinePosition ▪ BaseStyle ▪ ClippingStyle ▪ ColorFunctionScaling ▪ ColorFunction ▪ ContentSelectable ▪ CoordinatesToolOptions ▪ Epilog ▪ EvaluationMonitor ▪ Exclusions ▪ ExclusionsStyle ▪ Filling ▪ FillingStyle ▪ FormatType ▪ TraditionalForm ▪ Frame ▪ FrameLabel ▪ FrameStyle ▪ FrameTicks ▪ FrameTicksStyle ▪ GridLines ▪ GridLinesStyle ▪ ImageMargins ▪ ImagePadding ▪ ImageSize ▪ LabelingSize ▪ LabelStyle ▪ MaxRecursion ▪ Mesh ▪ MeshFunctions ▪ MeshShading ▪ MeshStyle ▪ Method ▪ PerformanceGoal ▪ $PerformanceGoal ▪ PlotHighlighting ▪ PlotLabel ▪ PlotLabels ▪ PlotLayout ▪ PlotLegends ▪ PlotPoints ▪ PlotRange ▪ Full ▪ PlotRangeClipping ▪ PlotRangePadding ▪ PlotRegion ▪ PlotStyle ▪ PlotTheme ▪ $PlotTheme ▪ PreserveImageOptions ▪ Prolog ▪ RegionFunction ▪ RotateLabel ▪ True ▪ None ▪ ScalingFunctions ▪ False ▪ TargetUnits ▪ Ticks ▪ TicksStyle ▪ WorkingPrecision ▪ MachinePrecision ▪ AbsArgPlot ▪ Total ▪ All ▪ ExternalTypeSignature ▪ Automatic ▪ Normal ▪ Transpose ▪ ItoProcess ▪ SystemModelExamples ▪ SystemModels ▪ SystemModelSimulate ▪ SystemModelMeasurements ▪ SystemModelSimulationData ▪ SystemModelSimulateSensitivity ▪ SystemModelPlot ▪ ParametricPlot ▪ SystemModel ▪ Plot ▪ ListLinePlot ▪ LogPlot ▪ SystemModelParametricSimulate ▪ ParametricFunction ▪ NMinimize ▪ FindMinimum ▪ NMaximize ▪ SystemModelLinearize ▪ FindSystemModelEquilibrium ▪ ConnectSystemModelController ▪ SystemModelReliability ▪ ReliabilityDistribution ▪ SurvivalFunction ▪ StructuralImportance ▪ ButterworthFilterModel ▪ Chebyshev1FilterModel ▪ BiquadraticFilterModel ▪ InputOutputResponse ▪ InputOutputResponseData ▪ RiccatiSolve ▪ DiscreteRiccatiSolve ▪ LyapunovSolve ▪ DiscreteLyapunovSolve ▪