Principal Axes of a Volume
To determine the orientation of a volume segment in space, you can calculate the second central moments of its density distribution and derive the corresponding eigenvectors. Here is a short script to compute central moments and volume orientation.
| In[1]:= |  X |
Define a function that calculates the moments of an array.
| In[2]:= |  X |
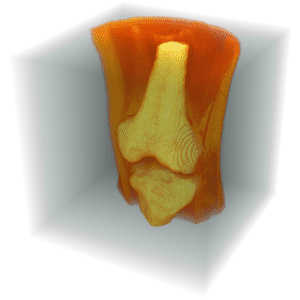
Convert the volume into a data array with its indices aligned to the graphics coordinates.
| In[3]:= | X |
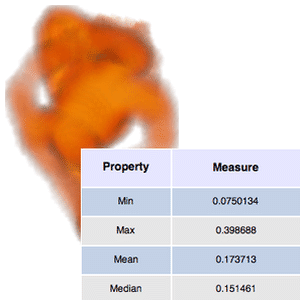
Compute the first- and second-order moments of the tooth density.
| In[4]:= | X |
| In[5]:= |  X |
Compute the principal axes of the central moments matrix.
| In[6]:= |  X |
| Out[6]= |
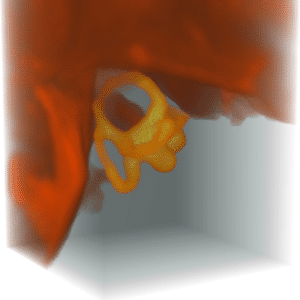
Display the principal axes of the tooth.
| Out[7]= | 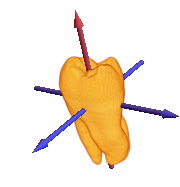 |