Application Areas
Wavelet Matrix Plot
Create matrix plots of the basis tree of the wavelet coefficients for discrete wavelet transforms of a matrix using either a pyramid or grid layout.
| In[1]:= |  X |
| Out[1]= | 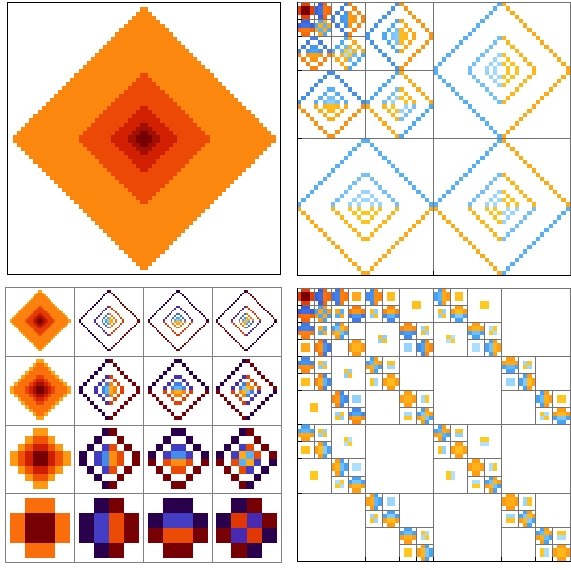 |
| New in Wolfram Mathematica 8: Wavelet Analysis | ◄ previous | next ► |
| In[1]:= |  X |
| Out[1]= |  |