Hydraulic Systems 

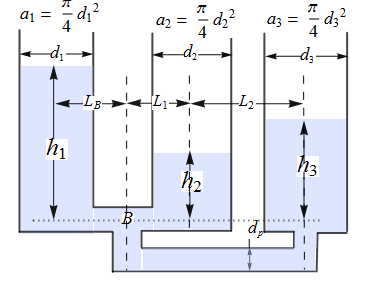
Model the change in height of water in three tanks, with the third tank leaking.

X \!\(\* GraphicsBox[{ {Thickness[0.005248074602497723], CapForm["Round"], JoinForm["Round"], StrokeForm[{RGBColor[0., 0., 0.], Opacity[0.73]}], EdgeForm[{ RGBColor[0., 0., 0.], Opacity[1.]}], EdgeForm[None], LineBox[{{0.32279580630701915`, 0.9257371759207741}, { 0.32279580630701915`, 0.264305231012697}, {0.5332719967832096, 0.264305231012697}, {0.5332719967832096, 0.8836566398377903}}]}, {EdgeForm[{RGBColor[0., 0., 0.], Opacity[0.], Thickness[ 0.005248074602497723], CapForm["Round"], JoinForm["Round"]}], FaceForm[{Hue[0.6277777777777778, 0.2972972972972973, 1.], Opacity[0.45]}], StyleBox[RectangleBox[{0.06527777777777777, 0.7680555555555555}, {0.3208333333333334, 0.16928294573643382`}], RectangleBoxOptions->{RoundingRadius->0}]}, {EdgeForm[{RGBColor[0., 0., 0.], Opacity[0.], Thickness[ 0.005248074602497723], CapForm["Round"], JoinForm["Round"]}], FaceForm[{Hue[0.6277777777777778, 0.2972972972972973, 1.], Opacity[0.45]}], StyleBox[RectangleBox[{0.5403746770025846, 0.45859173126614966`}, {0.8167312661498711, 0.18062015503875944`}], RectangleBoxOptions->{RoundingRadius->0}]}, {EdgeForm[{RGBColor[0., 0., 0.], Opacity[0.], Thickness[ 0.005248074602497723], CapForm["Round"], JoinForm["Round"]}], FaceForm[{Hue[0.6277777777777778, 0.2972972972972973, 1.], Opacity[0.45]}], StyleBox[RectangleBox[{0.3253229974160211, 0.2615956072351419}, {0.5372739018087855, 0.17955426356589108`}], RectangleBoxOptions->{RoundingRadius->0}]}, {Thickness[0.001122018454301963], CapForm["Round"], JoinForm["Round"], Arrowheads[{-0.02301441817408509, 0.02301441817408509}], StrokeForm[{RGBColor[0., 0., 0.], Opacity[0.91]}], EdgeForm[{ RGBColor[0., 0., 0.], Opacity[0.91], Thickness[ 0.005248074602497723], CapForm["Round"], JoinForm["Round"]}], FaceForm[{Hue[0.6277777777777778, 0.2972972972972973, 1.], Opacity[0.45]}], ArrowBox[{{0.8794250645994834, 0.12389648882808948`}, { 0.8794250645994834, 0.03722982216142259}}]}, {Thickness[0.0013031667784522986`], CapForm["Round"], JoinForm[ "Round"], StrokeForm[{RGBColor[0., 0., 0.], Opacity[0.99]}], EdgeForm[{RGBColor[0., 0., 0.], Opacity[1.]}], EdgeForm[None], LineBox[{{0.8781107992515375, 0.11505448825974597`}, { 0.8781107992515375, 0.1633636670037073}, {0.9056970061480892, 0.1633636670037073}}]}, {Thickness[0.0027542287033381634`], CapForm["Round"], JoinForm[ "Round"], Arrowheads[{-0.04, 0.04}], StrokeForm[{RGBColor[ 0., 0., 0.], Opacity[0.91]}], EdgeForm[{RGBColor[0., 0., 0.], Opacity[0.91], Thickness[0.005248074602497723], CapForm["Round"], JoinForm["Round"]}], FaceForm[{Hue[ 0.6277777777777778, 0.2972972972972973, 1.], Opacity[0.45]}], ArrowBox[{{0.1819444444444445, 0.770981182897169}, { 0.1819444444444445, 0.22005803730392082`}}]}, {Thickness[0.0010839269140212027`], CapForm["Round"], JoinForm[ "Round"], Arrowheads[{-0.031188895840939364`, 0.031188895840939364`}], StrokeForm[{RGBColor[0., 0., 0.], Opacity[0.9500000000000001]}], EdgeForm[{RGBColor[0., 0., 0.], Opacity[0.], Thickness[ 0.005248074602497723], CapForm["Round"], JoinForm["Round"]}], FaceForm[{Hue[0.6277777777777778, 0.2972972972972973, 1.], Opacity[0.45]}], ArrowBox[{{0.05972222222222223, 0.8097222222222223}, { 0.3236111111111112, 0.8097222222222223}}]}, {Thickness[0.0010839269140212027`], CapForm["Round"], JoinForm[ "Round"], Arrowheads[{-0.031188895840939364`, 0.031188895840939364`}], StrokeForm[{RGBColor[0., 0., 0.], Opacity[0.9500000000000001]}], EdgeForm[{RGBColor[0., 0., 0.], Opacity[0.], Thickness[ 0.005248074602497723], CapForm["Round"], JoinForm["Round"]}], FaceForm[{Hue[0.6277777777777778, 0.2972972972972973, 1.], Opacity[0.45]}], ArrowBox[{{0.9345952277543073, 0.8017441860465114}, { 1.2313694213026949`, 0.8017441860465114}}]}, InsetBox["", {0.1625, 0.4652777777777778}, {Left, Baseline}, Alignment->{Left, Top}], InsetBox[ StyleBox[ TagBox[ StyleBox[ SubscriptBox["h", "1"], FontSize->24], "RawBoxes"], FontWeight->Plain, Background->GrayLevel[ 1.]], {0.1569444444444445, 0.4458333333333333}, { Left, Baseline}, Alignment->{Left, Top}], InsetBox[ GraphicsBox[{}], {0.6583333333333334, 0.461111111111111}, { Left, Baseline}, Alignment->{Left, Top}], InsetBox[ StyleBox[ TagBox[ SubscriptBox[ StyleBox["d", FontSize->18], "p"], "RawBoxes"], FontWeight->Plain, Background->GrayLevel[ 1.]], {0.8765180878552973, 0.16850775193798428`}, { Left, Baseline}, Alignment->{Left, Top}], InsetBox[ StyleBox[ TagBox[ SubscriptBox[ StyleBox["d", FontSize->18], "1"], "RawBoxes"], FontWeight->Plain, Background->GrayLevel[ 1.]], {0.17361111111111116`, 0.7930555555555555}, { Left, Baseline}, Alignment->{Left, Top}], InsetBox[ StyleBox[ TagBox[ SubscriptBox[ StyleBox["d", FontSize->18], "3"], "RawBoxes"], FontWeight->Plain, Background->GrayLevel[1.]], {1.062855297157623, 0.7850775193798449}, { Left, Baseline}, Alignment->{Left, Top}], StyleBox[InsetBox[ StyleBox[ TagBox[ RowBox[{ SubscriptBox["a", "1"], "=", " ", RowBox[{ FractionBox["\[Pi]", "4"], SuperscriptBox[ SubscriptBox["d", "1"], "2"]}]}], "RawBoxes"], FontWeight->Plain, Background->GrayLevel[ 1.]], {0.06579457364341088, 0.9309108527131781}, { Left, Baseline}, Alignment->{Left, Top}], FontSize->18], StyleBox[InsetBox[ StyleBox[ TagBox[ RowBox[{ SubscriptBox["a", "3"], "=", " ", RowBox[{ FractionBox["\[Pi]", "4"], SuperscriptBox[ SubscriptBox["d", "3"], "2"]}]}], "RawBoxes"], FontWeight->Plain, Background->GrayLevel[1.]], {0.9436046511627911, 0.913049095607235}, { Left, Baseline}, Alignment->{Left, Top}], FontSize->18], {EdgeForm[{RGBColor[0., 0., 0.], Opacity[0.], Thickness[ 0.005248074602497723], CapForm["Round"], JoinForm["Round"]}], FaceForm[{Hue[0.6277777777777778, 0.2972972972972973, 1.], Opacity[0.45]}], StyleBox[RectangleBox[{0.9377906976744192, 0.576970284237726}, {1.2234496124031007`, 0.17496770025839767`}], RectangleBoxOptions->{RoundingRadius->0}]}, {Thickness[0.005248074602497723], CapForm["Round"], JoinForm["Round"], StrokeForm[{RGBColor[0., 0., 0.], Opacity[0.73]}], EdgeForm[{ RGBColor[0., 0., 0.], Opacity[1.]}], EdgeForm[None], LineBox[{{0.39224806201550394`, 0.17441860465116288`}, { 0.39224806201550394`, 0.0348837209302324}}]}, {Thickness[0.005248074602497723], CapForm["Round"], JoinForm["Round"], StrokeForm[{RGBColor[0., 0., 0.], Opacity[0.73]}], EdgeForm[{ RGBColor[0., 0., 0.], Opacity[1.]}], EdgeForm[None], LineBox[{{0.49457364341085286`, 0.1806201550387596}, { 0.49457364341085286`, 0.12170542635658887`}}]}, {Thickness[0.005248074602497723], CapForm["Round"], JoinForm["Round"], StrokeForm[{RGBColor[0., 0., 0.], Opacity[0.73]}], EdgeForm[{ RGBColor[0., 0., 0.], Opacity[1.]}], EdgeForm[None], LineBox[{{0.4976744186046515, 0.1806201550387596}, { 0.8139534883720936, 0.1806201550387596}}]}, {Thickness[0.005248074602497723], CapForm["Round"], JoinForm["Round"], StrokeForm[{RGBColor[0., 0., 0.], Opacity[0.73]}], EdgeForm[{ RGBColor[0., 0., 0.], Opacity[1.]}], EdgeForm[None], LineBox[{{0.39224806201550394`, 0.17751937984496124`}, { 0.06046511627906981, 0.17751937984496124`}}]}, {Thickness[0.005248074602497723], CapForm["Round"], JoinForm["Round"], StrokeForm[{RGBColor[0., 0., 0.], Opacity[0.73]}], EdgeForm[{ RGBColor[0., 0., 0.], Opacity[1.]}], EdgeForm[None], LineBox[{{0.06046511627907025, 0.8953488372093024}, { 0.06046511627907025, 0.17596899224806162`}}]}, {Thickness[0.005248074602497723], CapForm["Round"], JoinForm["Round"], StrokeForm[{RGBColor[0., 0., 0.], Opacity[0.73]}], EdgeForm[{ RGBColor[0., 0., 0.], Opacity[1.]}], EdgeForm[None], LineBox[{{0.4976744186046516, 0.11860465116279051`}, { 1.0341085271317834`, 0.11860465116279051`}}]}, {Thickness[0.005248074602497723], CapForm["Round"], JoinForm["Round"], StrokeForm[{RGBColor[0., 0., 0.], Opacity[0.73]}], EdgeForm[{ RGBColor[0., 0., 0.], Opacity[1.]}], EdgeForm[None], LineBox[{{0.39224806201550394`, 0.03643410852713136}, { 1.1116279069767456`, 0.03643410852713136}}]}, {Thickness[0.005248074602497723], CapForm["Round"], JoinForm["Round"], StrokeForm[{RGBColor[0., 0., 0.], Opacity[0.73]}], EdgeForm[{ RGBColor[0., 0., 0.], Opacity[1.]}], EdgeForm[None], LineBox[{{1.0372093023255817`, 0.17596899224806184`}, { 1.0372093023255817`, 0.12325581395348806`}}]}, {Thickness[0.005248074602497723], CapForm["Round"], JoinForm["Round"], StrokeForm[{RGBColor[0., 0., 0.], Opacity[0.73]}], EdgeForm[{ RGBColor[0., 0., 0.], Opacity[1.]}], EdgeForm[None], LineBox[{{1.12093023255814, 0.17286821705426347`}, { 1.1178294573643417`, 0.03573910719059049}}]}, {Thickness[0.005248074602497723], CapForm["Round"], JoinForm["Round"], StrokeForm[{RGBColor[0., 0., 0.], Opacity[0.73]}], EdgeForm[{ RGBColor[0., 0., 0.], Opacity[1.]}], EdgeForm[None], LineBox[{{1.2263565891472878`, 0.8860465116279069}, { 1.2263565891472878`, 0.17906976744185998`}}]}, {Thickness[0.005248074602497723], CapForm["Round"], JoinForm["Round"], StrokeForm[{RGBColor[0., 0., 0.], Opacity[0.73]}], EdgeForm[{ RGBColor[0., 0., 0.], Opacity[1.]}], EdgeForm[None], LineBox[{{0.9317829457364344, 0.17751937984496124`}, { 1.0372093023255822`, 0.17751937984496124`}}]}, {Thickness[0.005248074602497723], CapForm["Round"], JoinForm["Round"], StrokeForm[{RGBColor[0., 0., 0.], Opacity[0.73]}], EdgeForm[{ RGBColor[0., 0., 0.], Opacity[1.]}], EdgeForm[None], LineBox[{{1.1224806201550395`, 0.17286821705426303`}, { 1.2248062015503884`, 0.17286821705426303`}}]}, {Thickness[0.005248074602497723], CapForm["Round"], JoinForm["Round"], StrokeForm[{RGBColor[0., 0., 0.], Opacity[0.73]}], EdgeForm[{ RGBColor[0., 0., 0.], Opacity[1.]}], EdgeForm[None], LineBox[{{0.9317829457364352, 0.8829457364341083}, { 0.9317829457364352, 0.1759689922480614}}]}, {Thickness[0.005248074602497723], CapForm["Round"], JoinForm["Round"], StrokeForm[{RGBColor[0., 0., 0.], Opacity[0.73]}], EdgeForm[{ RGBColor[0., 0., 0.], Opacity[1.]}], EdgeForm[None], LineBox[{{0.813953488372094, 0.8891472868217051}, { 0.813953488372094, 0.18217054263565813`}}]}, {EdgeForm[{RGBColor[0., 0., 0.], Opacity[0.], Thickness[ 0.005248074602497723], CapForm["Round"], JoinForm["Round"]}], FaceForm[{Hue[0.6277777777777778, 0.2972972972972973, 1.], Opacity[0.45]}], StyleBox[RectangleBox[{0.3963501291989668, 0.17822997416020697`}, {0.4935723514211886, 0.03727390180878553}], RectangleBoxOptions->{RoundingRadius->0}]}, {EdgeForm[{RGBColor[0., 0., 0.], Opacity[0.], Thickness[ 0.005248074602497723], CapForm["Round"], JoinForm["Round"]}], FaceForm[{Hue[0.6277777777777778, 0.2972972972972973, 1.], Opacity[0.45]}], StyleBox[RectangleBox[{0.4986757105943158, 0.11931524547803596`}, {1.1137273901808789`, 0.03727390180878509}], RectangleBoxOptions->{RoundingRadius->0}]}, {EdgeForm[{RGBColor[0., 0., 0.], Opacity[0.], Thickness[ 0.005248074602497723], CapForm["Round"], JoinForm["Round"]}], FaceForm[{Hue[0.6277777777777778, 0.2972972972972973, 1.], Opacity[0.45]}], StyleBox[RectangleBox[{1.0382105943152462`, 0.17512919896640805`}, {1.1199289405684758`, 0.11789405684754478`}], RectangleBoxOptions->{RoundingRadius->0}]}, StyleBox[InsetBox[ StyleBox[ TagBox[ RowBox[{ SubscriptBox["a", "2"], "=", " ", RowBox[{ FractionBox["\[Pi]", "4"], SuperscriptBox[ SubscriptBox["d", "2"], "2"]}]}], "RawBoxes"], FontWeight->Plain, Background->GrayLevel[ 1.]], {0.5488372093023257, 0.9093023255813951}, { Left, Baseline}, Alignment->{Left, Top}], FontSize->18], {Thickness[0.0010839269140212027`], CapForm["Round"], JoinForm[ "Round"], Arrowheads[{-0.031188895840939364`, 0.031188895840939364`}], StrokeForm[{RGBColor[0., 0., 0.], Opacity[0.9500000000000001]}], EdgeForm[{RGBColor[0., 0., 0.], Opacity[0.], Thickness[ 0.005248074602497723], CapForm["Round"], JoinForm["Round"]}], FaceForm[{Hue[0.6277777777777778, 0.2972972972972973, 1.], Opacity[0.45]}], ArrowBox[{{0.5311151673577312, 0.8069767441860461}, { 0.8195518598641914, 0.8069767441860461}}]}, InsetBox[ StyleBox[ TagBox[ SubscriptBox[ StyleBox["d", FontSize->18], "2"], "RawBoxes"], FontWeight->Plain, Background->GrayLevel[ 1.]], {0.6449612403100777, 0.7945736434108527}, { Left, Baseline}, Alignment->{Left, Top}], {Thickness[0.0027542287033381634`], CapForm["Round"], JoinForm[ "Round"], Arrowheads[{-0.04, 0.04}], StrokeForm[{RGBColor[ 0., 0., 0.], Opacity[0.91]}], EdgeForm[{RGBColor[0., 0., 0.], Opacity[0.91], Thickness[0.005248074602497723], CapForm["Round"], JoinForm["Round"]}], FaceForm[{Hue[ 0.6277777777777778, 0.2972972972972973, 1.], Opacity[0.45]}], ArrowBox[{{0.666666666666667, 0.4679805432847771}, { 0.666666666666667, 0.2234697090046276}}]}, {Thickness[0.0027542287033381634`], CapForm["Round"], JoinForm[ "Round"], Arrowheads[{-0.04, 0.04}], StrokeForm[{RGBColor[ 0., 0., 0.], Opacity[0.91]}], EdgeForm[{RGBColor[0., 0., 0.], Opacity[0.91], Thickness[0.005248074602497723], CapForm["Round"], JoinForm["Round"]}], FaceForm[{Hue[ 0.6277777777777778, 0.2972972972972973, 1.], Opacity[0.45]}], ArrowBox[{{1.0728682170542643`, 0.5737001069782965}, { 1.0728682170542643`, 0.22090729862769343`}}]}, InsetBox[ StyleBox[ TagBox[ StyleBox[ SubscriptBox["h", "2"], FontSize->24], "RawBoxes"], FontWeight->Plain, Background->GrayLevel[ 1.]], {0.6387596899224808, 0.32945736434108497`}, { Left, Baseline}, Alignment->{Left, Top}], InsetBox[ StyleBox[ TagBox[ StyleBox[ SubscriptBox["h", "3"], FontSize->24], "RawBoxes"], FontWeight->Plain, Background->GrayLevel[1.]], {1.051162790697675, 0.3852713178294571}, { Left, Baseline}, Alignment->{Left, Top}], {Thickness[0.005248074602497723], Dashing[{0, Small}], CapForm[ "Round"], JoinForm["Round"], StrokeForm[{RGBColor[0., 0., 0.], Opacity[0.77]}], EdgeForm[{RGBColor[0., 0., 0.], Opacity[1.]}], EdgeForm[None], LineBox[{{0.110077519379845, 0.2178294573643409}, { 1.1364341085271323`, 0.2178294573643409}}]}, InsetBox["", {0.4170542635658916, 0.20852713178294557`}, { Left, Baseline}, Alignment->{Left, Top}], InsetBox["", {0.41705426356589154`, 0.20232558139534884`}, { Left, Baseline}, Alignment->{Left, Top}], InsetBox[ StyleBox[ TagBox["B", "RawBoxes"], FontSize->18, FontWeight->Plain, FontSlant->"Italic", Background->GrayLevel[ 1.]], {0.4263565891472869, 0.20232558139534884`}, { Left, Baseline}, Alignment->{Left, Top}], {Thickness[0.0023713737056616554`], Dashing[{Medium, Medium}], CapForm["Round"], JoinForm["Round"], StrokeForm[{RGBColor[ 0., 0., 0.], Opacity[0.98]}], EdgeForm[{RGBColor[0., 0., 0.], Opacity[1.]}], EdgeForm[None], LineBox[{{0.44186046511627924`, 0.7294573643410854}, { 0.44186046511627924`, 0.04108527131782935}}]}, {Thickness[0.0023713737056616554`], Dashing[{Medium, Medium}], CapForm["Round"], JoinForm["Round"], StrokeForm[{RGBColor[ 0., 0., 0.], Opacity[0.98]}], EdgeForm[{RGBColor[0., 0., 0.], Opacity[1.]}], EdgeForm[None], LineBox[{{1.0713178294573649`, 0.7325581395348837}, { 1.0744186046511632`, 0.04418604651162772}}]}, {Thickness[0.0023713737056616554`], Dashing[{Medium, Medium}], CapForm["Round"], JoinForm["Round"], StrokeForm[{RGBColor[ 0., 0., 0.], Opacity[0.98]}], EdgeForm[{RGBColor[0., 0., 0.], Opacity[1.]}], EdgeForm[None], LineBox[{{0.6651162790697676, 0.7325581395348839}, { 0.6651162790697676, 0.1682170542635657}}]}, {Thickness[0.0027542287033381634`], CapForm["Round"], JoinForm[ "Round"], Arrowheads[{-0.04, 0.04}], StrokeForm[{RGBColor[ 0., 0., 0.], Opacity[0.91]}], EdgeForm[{RGBColor[0., 0., 0.], Opacity[0.91], Thickness[0.005248074602497723], CapForm["Round"], JoinForm["Round"]}], FaceForm[{Hue[ 0.6277777777777778, 0.2972972972972973, 1.], Opacity[0.45]}], ArrowBox[{{0.6702720308307804, 0.6348837209302325}, { 0.4412365658088681, 0.6348837209302325}}]}, {Thickness[0.0027542287033381634`], CapForm["Round"], JoinForm[ "Round"], Arrowheads[{-0.04, 0.04}], StrokeForm[{RGBColor[ 0., 0., 0.], Opacity[0.91]}], EdgeForm[{RGBColor[0., 0., 0.], Opacity[0.91], Thickness[0.005248074602497723], CapForm["Round"], JoinForm["Round"]}], FaceForm[{Hue[ 0.6277777777777778, 0.2972972972972973, 1.], Opacity[0.45]}], ArrowBox[{{1.0706538819434517`, 0.6333333333333331}, { 0.6682942812292811, 0.6333333333333331}}]}, InsetBox[ StyleBox[ TagBox[ StyleBox[ SubscriptBox["L", "1"], FontSize->16], "RawBoxes"], FontWeight->Plain, Background->GrayLevel[ 1.]], {0.5348837209302326, 0.6209302325581396}, { Left, Baseline}, Alignment->{Left, Top}], InsetBox[ StyleBox[ TagBox[ StyleBox[ SubscriptBox["L", "2"], FontSize->16], "RawBoxes"], FontWeight->Plain, Background->GrayLevel[ 1.]], {0.8418604651162793, 0.6209302325581396}, { Left, Baseline}, Alignment->{Left, Top}], {Thickness[0.0027542287033381634`], CapForm["Round"], JoinForm[ "Round"], Arrowheads[{-0.04, 0.04}], StrokeForm[{RGBColor[ 0., 0., 0.], Opacity[0.91]}], EdgeForm[{RGBColor[0., 0., 0.], Opacity[0.91], Thickness[0.005248074602497723], CapForm["Round"], JoinForm["Round"]}], FaceForm[{Hue[ 0.6277777777777778, 0.2972972972972973, 1.], Opacity[0.45]}], ArrowBox[{{0.4408692166486482, 0.6333333333333331}, { 0.18707316081355613`, 0.6333333333333331}}]}, InsetBox[ StyleBox[ TagBox[ StyleBox[ SubscriptBox["L", "B"], FontSize->16], "RawBoxes"], FontWeight->Plain, Background->GrayLevel[ 1.]], {0.2899224806201551, 0.6209302325581396}, { Left, Baseline}, Alignment->{Left, Top}]}, ContentSelectable->True, ImagePadding->{{0., 0.}, {0., 0.}}, ImageSize->{378.55078125, 281.}, PlotRange->{{0., 1.3333333333333335`}, {0., 1.}}, PlotRangePadding->Automatic]\)

The pressures at the bottoms of the tanks 1, 2, and 3 are represented as , , and , respectively. The pipe from tank 1 branches off to tanks 2 and 3. The pressure at the pipe branch is given as . Flow rates depend on pressure differences and geometry.

In[1]:=

X flowRate1B = (Subscript[p, 1][t] - Subscript[p, B][t]) (\[Pi] Subscript[d, p]^4)/( 128 \[Mu] Subscript[L, B]); flowRateB2 = (Subscript[p, B][t] - Subscript[p, 2][t]) (\[Pi] Subscript[d, p]^4)/( 128 \[Mu] Subscript[L, 1]); flowRateB3 = (Subscript[p, B][t] - Subscript[p, 3][t]) (\[Pi] Subscript[d, p]^4)/( 128 \[Mu] Subscript[L, 2]);

All the fluid leaving tank 1 should enter tank 2 and tank 3. This is represented as a constraint. Also, the height of the fluid in the tanks is related to the pressure in the tank by Toricelli's law.

In[2]:=

X flowRateConstraint = (flowRate1B == flowRateB2 + flowRateB3); pressureEqns = {Subscript[p, 1][t] == \[Rho] g Subscript[h, 1][t], Subscript[p, 2][t] == \[Rho] g Subscript[h, 2][t], Subscript[p, 3][t] == \[Rho] g Subscript[h, 3][t]};

The rate at which the fluid leaves or enters the tank (i.e. flow rate) is directly proportional to the rate of change of the height of the fluid in the tank. This relation comes through mass conservation of incompressible fluids.

In[3]:=

X massConservation = {Subscript[a, 1] Subscript[h, 1]'[t] == -flowRate1B, Subscript[a, 2] Subscript[h, 2]'[t] == flowRateB2, Subscript[a, 3] Subscript[h, 3]'[t] == flowRateB3 - Subscript[a, 3] Subscript[h, 3][t]/10};

Specify the dimensions and parameters associated with the system. The cross-sectional areas of tanks 1, 2, and 3 are specified by , , and , respectively. The density and viscosity of the fluid are specified as (kg/m³) and (kg/m-s), respectively.

In[4]:=

X params = {Subscript[a, 1] -> 1, Subscript[a, 2] -> 1, Subscript[a, 3] -> 1, Subscript[L, B] -> 0.1, Subscript[L, 1] -> 0.1, Subscript[L, 2] -> 0.2, Subscript[d, p] -> 0.2, \[Rho] -> .2, \[Mu] -> 2 10^-3, g -> 9.81};

Specify the initial heights of the fluid in each tank.

In[5]:=

X ics = {Subscript[h, 1][0] == 1, Subscript[h, 2][0] == 0, Subscript[h, 3][0] == 0};

Solve and visualize the result.

In[6]:=

X tankSol = NDSolve[{pressureEqns, massConservation, flowRateConstraint, ics} /. params, {Subscript[h, 1], Subscript[h, 2], Subscript[h, 3]}, {t, 0, 90}];

In[7]:=

X Plot[Evaluate[{Subscript[h, 1][t], Subscript[h, 2][t], Subscript[h, 3][t]} /. tankSol], {t, 0, 90}, PlotRange -> All, ImageSize -> 300, PlotStyle -> {Red, Blue, Magenta}, PlotLegends -> LineLegend[Automatic, {"Tank 1", "Tank 2", "Tank 3"}, LegendFunction -> "Panel", LegendMargins -> 10]]

Out[7]=