Model Constrained Systems as DAEs
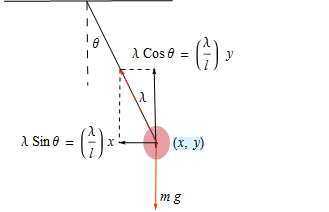
Model the motion of a single pendulum.
 X |
Derive the governing equations using Newton's second law of motion, 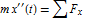 and
and 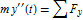 .
.
| In[1]:= | X |
Express the fixed length of the pendulum rod as an algebraic constraint.
| In[2]:= | X |
The pendulum is released from the horizontal position with a vertical velocity of 1.
| In[3]:= | X |
Specify the physical parameters for the pendulum system.
| In[4]:= | X |
Solve the high-index DAE and visualize the system.
| In[5]:= |  X |
| In[6]:= |  X |
| Out[6]= | 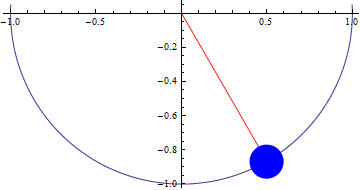 |