Slider-Crank Mechanism 

In[7]:=

X bar[loc_: {0, 0}, rotate_: 0, scale_: 1, length_: 1, width_: .1, color_: Hue[.6, .2, .9]] := Module[{}, GraphicsGroup[{ Rotate[{ color, EdgeForm[Directive[Black, AbsoluteThickness[.5]]], (* polygon instead of rounded rectangle in case texture is needed \ *) Polygon[ Flatten[{Table[ loc + scale {width Sin[ a Pi], width Cos[a Pi]}, {a, 1, 2, 1/16}], Table[{length, 0} + loc + scale {width Sin[ a Pi], width Cos[a Pi]}, {a, 0, 1, 1/16}]}, 1]], AbsolutePointSize[5], Black, Point[loc], Point[loc + scale {length, 0}] }, rotate Degree, loc] }] ];

In[8]:=

X barFlange[loc_: {0, 0}, rotate_: 0, scale_: 1, length_: 1, width_: .1, size1_: 1, size2_: 1, color_: Hue[.6, .2, .9]] := Module[{}, GraphicsGroup[{ Rotate[{ color, EdgeForm[Directive[Black, AbsoluteThickness[.5]]], Polygon[ {loc + scale {0, -width size1 }, loc + scale {0, width size1 }, loc + scale {length, width size2 }, loc + scale {length, -width size2 }}], Lighter[color, .5], Disk[loc, scale width size1], Disk[loc + scale {length, 0}, scale width size2], (* pins *) Gray, Disk[loc, .4 scale width size1], Disk[loc + scale {length, 0}, .4 scale width size2] }, rotate Degree, loc] }] ];

In[9]:=

X dimensionLine[loc_: {0, 0}, rotate_: 0, scale_: 1, text_: "1", length_: 1, offset_: {0, 0}] := Module[{}, GraphicsGroup[{ Rotate[{ Black, AbsoluteThickness[.5], Line[{offset + loc + scale {0, 0}, offset + loc + scale {0, .1}}], Arrowheads[{-Small, Small}], Arrow[{offset + loc + scale {0, .05}, offset + loc + scale {length, .05}}], Line[{offset + loc + scale {length, 0}, offset + loc + scale {length, .1}}], Text[text, offset + loc + scale {length/2, .05}, Background -> White] }, rotate Degree, loc] }] ];

In[10]:=

X fixedHinge[loc_: {0, 0}, rotate_: 0, scale_: 1] := Module[{}, GraphicsGroup[{ Rotate[{ GrayLevel[.85], EdgeForm[Directive[Black, AbsoluteThickness[.5]]], Polygon[ Flatten[{{loc + scale {-.25, -.5}}, Table[loc + scale {.15 Sin[ a Pi], .15 Cos[a Pi]}, {a, 1.55, 2.45, .9/16}], {loc + scale {.25, -.5}}}, 1]], GrayLevel[.7], EdgeForm[], Rectangle[loc + scale {-.5, -.75}, loc + scale {.5, -.5}], Black, AbsoluteThickness[.5], Line[{loc + scale {-.5, -.5}, loc + scale {.5, -.5}}], AbsolutePointSize[5], Black, Point[{0, 0}] }, rotate Degree, loc] }] ];

In[11]:=

X slider[loc_: {0, 0}, rotate_: 0, scale_: 1, length_: 1, width_: .1, fixedLength_: 2, pos_: {0, 0}, color_: Hue[0, .2, .9]] := Module[{}, GraphicsGroup[{ Rotate[{ color, EdgeForm[{Black, AbsoluteThickness[.5]}], Rectangle[loc + pos + scale {-length, -width}, loc + pos + scale {length, width}], GrayLevel[.7], EdgeForm[], Rectangle[loc + scale {-fixedLength length, -width - .25}, loc + scale {fixedLength length, -width}], Black, AbsoluteThickness[.5], Line[{loc + scale {-fixedLength length, -width}, loc + scale {fixedLength length, -width}}], GrayLevel[.7], EdgeForm[], Rectangle[loc + scale {-fixedLength length, width + .25}, loc + scale {fixedLength length, width}], Black, AbsoluteThickness[.5], Line[{loc + scale {-fixedLength length, width}, loc + scale {fixedLength length, width}}] }, rotate Degree, loc] }] ];

In[12]:=

X plot1 = Plot[ Evaluate[{\[Lambda]1[t], \[Lambda]2[t]} /. sliderCrank], {t, 0, 10}, PlotStyle -> None, PlotLegends -> Placed[LineLegend[{Red, Blue}, {"Tension in Crank (\[Lambda]1)", "Tension in Connecting Rod (\[Lambda]2)"}], Bottom], ImageSize -> 300]; Animate[ rotate = (\[Alpha]1[t] /. sliderCrank)*(180/Pi); f1 = Graphics[{Red, Line[Map[Function[Evaluate[{#, \[Lambda]1[#]} /. sliderCrank]], Range[0, t, 0.025]]]}]; f2 = Graphics[{Blue, Line[Map[Function[Evaluate[{#, \[Lambda]2[#]} /. sliderCrank]], Range[0, t, 0.025]]]}]; {bLength, bfLength} = ({L1, L2} /. params)*0.3; Column[{ Graphics[{ (* parts *) bfAngle = ArcSin[bLength Cos[(90 - rotate) \[Degree]]/bfLength]*180/Pi; sliderLoc = {bLength Cos[rotate Pi/180] + bfLength Cos[bfAngle \[Degree]], 0}; slider[{.7, 0}, 0, .2, .7, .3, 3.5, sliderLoc - {.7, 0}, Hue[.05, .3, .9]], bar[{0, 0}, rotate, 1, bLength, .04, Hue[.6, .2, .7]], fixedHinge[{0, 0}, 0, .2], bfLoc = {bLength Sin[(90 - rotate) \[Degree]], bLength Cos[(90 - rotate) \[Degree]]}; barFlange[bfLoc, -bfAngle, 1, bfLength, .04, 2, 1.2, Hue[.6, .2, .9]], (* axis *) Black, AbsoluteThickness[.5], Arrowheads[Medium], Arrow[{{-.25, 0}, {.5, 0}}],(* x *) Arrow[{{0, -.05}, {0, .5}}],(* y *) (* dimensions *) , (* force arrow *) Opacity[1], Hue[0, 1, .8], AbsoluteThickness[2], Arrowheads[Medium], Arrow[{sliderLoc + {.35, 0}, sliderLoc + {.15, 0}}], Black, Text[Style["F(t)", 12, Italic], sliderLoc + {.37, 0}, {-1, 0}] }, PlotRange -> {{-.5, 1.5}, {-.5, .5}}, ImageSize -> 400] , Show[plot1, f1, f2]}, Alignment -> Center] , {t, 0, 10}, SaveDefinitions -> True, AnimationRunning -> False]

Model the motion of a simple slider-crank mechanism subject to an external force.

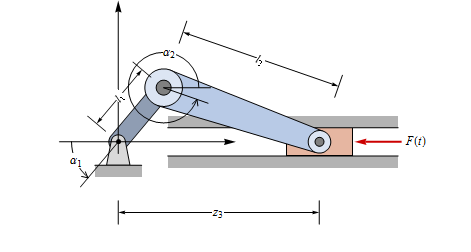X \!\(\* GraphicsBox[{GraphicsGroupBox[GeometricTransformationBox[ {Hue[0.05, 0.3, 0.9], EdgeForm[{GrayLevel[0], AbsoluteThickness[ 0.5]}], RectangleBox[{0.7140365793403993, -0.06}, \ {0.9940365793403994, 0.06}], {GrayLevel[0.7], EdgeForm[None], RectangleBox[{0.20999999999999996`, -0.11000000000000001`}, \ {1.19, -0.06}], {GrayLevel[0], AbsoluteThickness[0.5], LineBox[{{0.20999999999999996`, -0.06}, {1.19, -0.06}}], {GrayLevel[0.7], EdgeForm[None], RectangleBox[{0.20999999999999996`, 0.11000000000000001`}, \ {1.19, 0.06}], {GrayLevel[0], AbsoluteThickness[0.5], LineBox[{{0.20999999999999996`, 0.06}, {1.19, 0.06}}]}}}}}, {{{1, 0}, {0, 1}}, {0., 0.}}]], GraphicsGroupBox[GeometricTransformationBox[ {Hue[0.6, 0.2, 0.7], EdgeForm[{GrayLevel[0], AbsoluteThickness[0.5]}], PolygonBox[CompressedData[" 1:eJxTTMoPSmViYGBQAmIQDQPVIuvcH1Yt2c/88lzium/1+z1SfHYoiy3ZP29p L0dJZP9+n6smcqdeL9pvbMJRO/ngtP3abanzvdkX7r/D8t+/99scOA0Th6mD 6YOZAzMXZg/MXpg70OTt0fTbo5lvj2a/PZr77NHcb4/mP3s0/9sbg8Flexj/ et6uN7ybL9vD1CcsKL/8T/cKzF32ZduYs33mX4G5y75R2ZhjDtNVmLvsfzyW Xy4TctUe7t6zP8vWTLgKc5f9nv02q75vvQpzl/2hrxox/Yeuwt2FJr8fTf9+ NPP3o9m/H819+9Hcvx/Nf/vR/L8fAN4bAVc= "]], {GrayLevel[0], AbsolutePointSize[5], PointBox[{0, 0}], PointBox[{0.3, 0}]}}, {{{ 0.6427876096865393, -0.766044443118978}, {0.766044443118978, 0.6427876096865393}}, {0, 0}}]], GraphicsGroupBox[GeometricTransformationBox[ {GrayLevel[0.85], EdgeForm[{GrayLevel[0], AbsoluteThickness[0.5]}], PolygonBox[CompressedData[" 1:eJxTTMoPSmViYGAQBmIQPWsmCKzcD6F37o9ImOJWHz5v/+SUvK0MlsX2ukxV FxzZ5u6fZNEZqavYYr/10OfKaWdn7X/PMvFPBGufffqR/zON90/fz9P8L0Go drJ9CF/s/PLPk/e3PK3IEo6Zbt/0cXqzr2D//j1H9++52DDLvu30scjPzq37 S/nmL7G5NMc+bYnwYqFZpftTjl0pvWE7z361wP/InI8Je3bItb4O3DHPPhQi b58Kla+H6LevgOrvgJhvvwtqfhjEfvsmqP0pEPfZ80PdtwXifvvvUPdrQfxn vwLqP6j/7Vuh/oeGjz0sfABj1Jnp "]], {GrayLevel[0.7], EdgeForm[None], RectangleBox[{-0.1, -0.15000000000000002`}, {0.1, -0.1}], {GrayLevel[0], AbsoluteThickness[0.5], LineBox[{{-0.1, -0.1}, {0.1, -0.1}}], {GrayLevel[0], AbsolutePointSize[5], PointBox[{0, 0}]}}}}, {{{1, 0}, { 0, 1}}, {0, 0}}]], GraphicsGroupBox[GeometricTransformationBox[ {Hue[0.6, 0.2, 0.9], EdgeForm[{GrayLevel[0], AbsoluteThickness[0.5]}], PolygonBox[{{0.19283628290596178`, 0.14981333293569338`}, { 0.19283628290596178`, 0.3098133329356934}, { 0.8928362829059617, 0.2778133329356934}, {0.8928362829059617, 0.1818133329356934}}], {RGBColor[0.8600000000000001, 0.8960000000000001, 0.95], DiskBox[{0.19283628290596178`, 0.2298133329356934}, 0.08], DiskBox[{0.8928362829059617, 0.2298133329356934}, 0.048]}, {GrayLevel[0.5], DiskBox[{0.19283628290596178`, 0.2298133329356934}, 0.032], DiskBox[{0.8928362829059617, 0.2298133329356934}, 0.0192]}}, {{{0.9445718520491966, 0.32830476133670483`}, {-0.32830476133670483`, 0.9445718520491966}}, {-0.06476025340225089, 0.07604719725552594}}]], {GrayLevel[0], AbsoluteThickness[0.5], Arrowheads[Medium], ArrowBox[{{-0.25, 0}, {0.5, 0}}], ArrowBox[{{0, -0.05}, {0, 0.6}}], { GraphicsGroupBox[GeometricTransformationBox[ {GrayLevel[0], AbsoluteThickness[0.5], LineBox[{{0, 0.07}, {0, 0.17}}], {Arrowheads[{-Small, Small}], ArrowBox[{{0, 0.12000000000000001`}, {0.3, 0.12000000000000001`}}], LineBox[{{0.3, 0.07}, {0.3, 0.17}}], InsetBox[ StyleBox["\<\"\\!\\(\\*SubscriptBox[\\(l\\), \\(1\\)]\\)\"\>", StripOnInput->False, FontSize->12], {0.15, 0.12000000000000001`}, Background->GrayLevel[1]]}}, {{{ 0.6427876096865393, -0.766044443118978}, {0.766044443118978, 0.6427876096865393}}, {0, 0}}]], GraphicsGroupBox[GeometricTransformationBox[ {GrayLevel[0], AbsoluteThickness[0.5], LineBox[{{0.19283628290596178`, 0.4298133329356934}, { 0.19283628290596178`, 0.5298133329356934}}], {Arrowheads[{-Small, Small}], ArrowBox[{{0.19283628290596178`, 0.4798133329356934}, { 0.8928362829059617, 0.4798133329356934}}], LineBox[{{0.8928362829059617, 0.4298133329356934}, { 0.8928362829059617, 0.5298133329356934}}], InsetBox[ StyleBox["\<\"\\!\\(\\*SubscriptBox[\\(l\\), \\(2\\)]\\)\"\>", StripOnInput->False, FontSize->12], {0.5428362829059618, 0.4798133329356934}, Background->GrayLevel[1]]}}, {{{0.9445718520491966, 0.32830476133670483`}, {-0.32830476133670483`, 0.9445718520491966}}, {-0.06476025340225089, 0.07604719725552594}}]], GraphicsGroupBox[GeometricTransformationBox[ {GrayLevel[0], AbsoluteThickness[0.5], LineBox[{{0, -0.35}, {0, -0.24999999999999997`}}], {Arrowheads[{-Small, Small}], ArrowBox[{{0, -0.3}, {0.8540365793403993, -0.3}}], LineBox[{{0.8540365793403993, -0.35}, { 0.8540365793403993, -0.24999999999999997`}}], InsetBox[ StyleBox["\<\"\\!\\(\\*SubscriptBox[\\(z\\), \\(3\\)]\\)\"\>", StripOnInput->False, FontSize->12], {0.42701828967019967`, -0.3}, Background->GrayLevel[1]]}}, {{{1, 0}, {0, 1}}, {0., 0.}}]], {GrayLevel[0], AbsoluteThickness[0.5], GeometricTransformationBox[ LineBox[{{0, 0}, {-0.25, 0}}], {{{ 0.6427876096865393, -0.766044443118978}, {0.766044443118978, 0.6427876096865393}}, {0, 0}}], CircleBox[{0, 0}, 0.2, NCache[{Pi, Rational[23, 18] Pi}, {3.141592653589793, 4.014257279586958}]], GeometricTransformationBox[ LineBox[{ Offset[{-3, 6}, {-0.2, 0}], Offset[{0, 0}, {-0.2, 0}], Offset[{3, 6}, {-0.2, 0}]}], {{{ 0.6427876096865393, -0.766044443118978}, {0.766044443118978, 0.6427876096865393}}, {0, 0}}], {GrayLevel[0], InsetBox[ StyleBox["\<\"\\!\\(\\*SubscriptBox[\\(\[Alpha]\\), \\(1\\)]\\)\"\>", StripOnInput->False, FontSize->12], {-0.2, -0.08}, {-1, 0}, Background->GrayLevel[1]], LineBox[{{0.19283628290596178`, 0.2298133329356934}, { 0.3928362829059618, 0.2298133329356934}}], GeometricTransformationBox[ LineBox[{{0.19283628290596178`, 0.2298133329356934}, { 0.3928362829059618, 0.2298133329356934}}], {{{ 0.9445718520491966, 0.32830476133670483`}, {-0.32830476133670483`, 0.9445718520491966}}, {-0.06476025340225089, 0.07604719725552594}}], CircleBox[{0.19283628290596178`, 0.2298133329356934}, 0.15, { 0, 5.948677009576}], GeometricTransformationBox[ LineBox[{ Offset[{-3, -6}, {0.3428362829059618, 0.2298133329356934}], Offset[{0, 0}, {0.3428362829059618, 0.2298133329356934}], Offset[{3, -6}, {0.3428362829059618, 0.2298133329356934}]}], {{{0.9445718520491964, 0.3283047613367053}, {-0.3283047613367053, 0.9445718520491964}}, {-0.06476025340225089, 0.07604719725552606}}]}, {GrayLevel[0], InsetBox[ StyleBox["\<\"\\!\\(\\*SubscriptBox[\\(\[Alpha]\\), \\(2\\)]\\)\"\>", StripOnInput->False, FontSize->12], {0.19283628290596178`, 0.3798133329356934}, {-1, 0}, Background->GrayLevel[1]]}}}}, {Hue[0, 1, 0.8], AbsoluteThickness[2], Opacity[1], Arrowheads[Medium], ArrowBox[{{1.2040365793403993`, 0}, {1.0040365793403994`, 0}}], {GrayLevel[0], InsetBox[ StyleBox["\<\"F(t)\"\>", StripOnInput->False, FontSize->12, FontSlant->Italic], {1.2240365793403993`, 0}, {-1, 0}]}}}, ImageSize->{470.6796875, Automatic}, PlotRange->{{-0.5, 1.5}, {-0.47, 0.6}}]\)

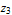The state of the slider-crank mechanism can be described completely by two angles ₁, ₂ and the distance of the slider from origin.

In[1]:=

X vars = {\[Alpha]1, \[Alpha]2, z, \[Lambda]1, \[Lambda]2};

Define the force that is exerted on the slider.

In[2]:=

X F[t] := -1;

The equations of motion are derived by resolving the forces and applying Newton's law 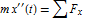and 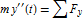. The crank and connecting rod have mass and therefore inertia.

In[3]:=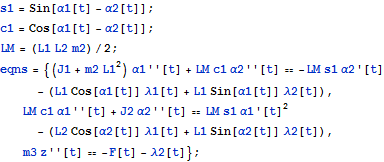

X s1 = Sin[\[Alpha]1[t] - \[Alpha]2[t]]; c1 = Cos[\[Alpha]1[t] - \[Alpha]2[t]]; LM = (L1 L2 m2)/2; eqns = {(J1 + m2 L1^2) \[Alpha]1''[t] + LM c1 \[Alpha]2''[t] == -LM s1 \[Alpha]2'[t] - (L1 Cos[\[Alpha]1[t]] \[Lambda]1[t] + L1 Sin[\[Alpha]1[t]] \[Lambda]2[t]), LM c1 \[Alpha]1''[t] + J2 \[Alpha]2''[t] == LM s1 \[Alpha]1'[t]^2 - (L2 Cos[\[Alpha]2[t]] \[Lambda]1[t] + L1 Sin[\[Alpha]2[t]] \[Lambda]2[t]), m3 z''[t] == -F[t] - \[Lambda]2[t]};

The algebraic equations define the geometry of the system.

In[4]:=

X constraints = ({ {L1 Sin[\[Alpha]1[t]] + L2 Sin[\[Alpha]2[t]] == 0}, {z[t] - L1 Cos[\[Alpha]1[t]] - L2 Cos[\[Alpha]2[t]] == 0} });

Define the physical parameters for the system. Here 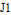and 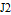are the moment of inertia.

In[5]:=

X params = {J1 -> 4.5, J2 -> 5.5, m1 -> 1, m2 -> 1, m3 -> 1, L1 -> 1, L2 -> 2, g -> 9.81};

Solve and visualize the system.

In[6]:=

X {sliderCrank} = NDSolve[{eqns, constraints, \[Alpha]1[0] == Pi/4, \[Alpha]1'[0] == -1} /. params, vars, {t, 0, 20}, Method -> {"IndexReduction" -> Automatic}];

Play Animation » Stop Animation »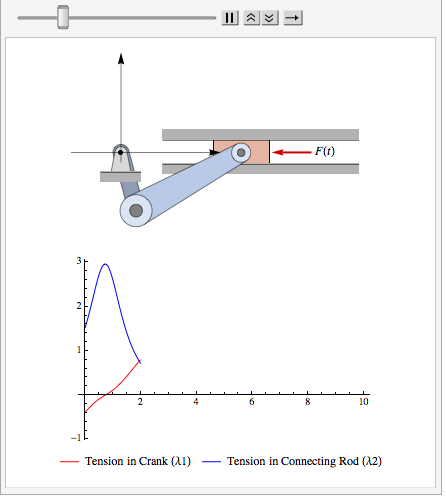